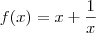 . Prove que
. Prove que , para todo
, para todo 
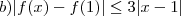 , para
, para 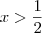
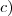 Use
Use  e
e  para provar por
para provar por  e
e  que f é contínua em x=1
que f é contínua em x=1Eu pensei em algo que pudesse ajudar na resolução do item a). Foi o seguinte:
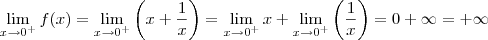
Como
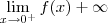 , temos, pela definição de limites laterais e pela definição de limites no infinito, que:
, temos, pela definição de limites laterais e pela definição de limites no infinito, que: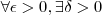 tal que
tal que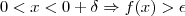 , ou seja:
, ou seja: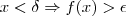
Mas eu não sei como, e nem se é possível, usar esse resultado para provar a afirmação do item a).
Alguém pode me ajudar?


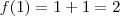 , e daí
, e daí 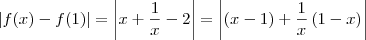 . Agora usando a desigualdade triangular:
. Agora usando a desigualdade triangular:
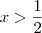 temos
temos 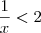 e daí
e daí 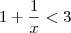 , e portanto pelo item a) concluimos
, e portanto pelo item a) concluimos 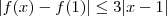 .
.

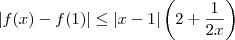
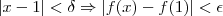

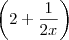
 e analisar o comportamento de
e analisar o comportamento de 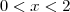 . Mas essa função vai pro infinito para valores de x próximos de 0.
. Mas essa função vai pro infinito para valores de x próximos de 0. , podemos encontrar
, podemos encontrar 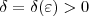 tal que
tal que 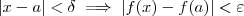 . Pelo item b), isto nos sugere que tomemos
. Pelo item b), isto nos sugere que tomemos 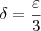 . Assim, teremos que pelo item b que:
. Assim, teremos que pelo item b que: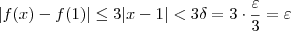
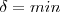
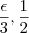 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)