 por celso alexandre » Seg Out 03, 2011 16:41
por celso alexandre » Seg Out 03, 2011 16:41
Matematica financeira - a questao e essa? um titulo vencivel em 4 meses apresenta um valor de resgate de R$407.164,90 é prposta a troca deste titulo por outro de R$480.000,00 vencivel daqui a 8 meses. sendo de 5% am a rentabilidade exigida pelo aplicador, avalie se a troca e vantajosa?
as formulas aprendidas e aplicadas e juros simples, juros composto, montante, taxas aparente real e inflacionaria, formula do antecipado,, ai vem minha pergunta qual dessas formulas se aplicam.. ou qual formula aplicar?
-
celso alexandre
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 27, 2011 16:32
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por mausim » Qua Out 26, 2011 14:55
por mausim » Qua Out 26, 2011 14:55
celso alexandre escreveu:Matematica financeira - a questao e essa? um titulo vencivel em 4 meses apresenta um valor de resgate de R$407.164,90 é prposta a troca deste titulo por outro de R$480.000,00 vencivel daqui a 8 meses. sendo de 5% am a rentabilidade exigida pelo aplicador, avalie se a troca e vantajosa?
as formulas aprendidas e aplicadas e juros simples, juros composto, montante, taxas aparente real e inflacionaria, formula do antecipado,, ai vem minha pergunta qual dessas formulas se aplicam.. ou qual formula aplicar?
Bem, eu faria assim:
Quanto vale o título hoje, esse que vai vencer daqui a 4 meses?
Se a taxa que o emprestador acha exige é de 5%am, então a fórmula a ser usada para isto é a do Montante, invertendo sua utilização para cálculo do valor presente:
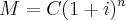
Como desejamos o valor da aplicação, no caso o "C", temos
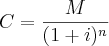
isto é
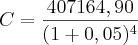
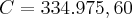
que é o valor presente.
Este valor presente seria fruto de uma nova aplicação, para daqui a 8 meses.
Se o aplicador exige os mesmos 5%am, teríamos de novo a fórmula do montante com esta aplicação
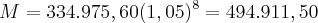
Como este valor é superior ao oferecido no novo contrato (480.000,00), não será um bom negócio trocar.
-
mausim
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Out 25, 2011 10:27
- Formação Escolar: SUPLETIVO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ME AJUDE
por ursoforte » Seg Ago 15, 2011 10:33
- 1 Respostas
- 1684 Exibições
- Última mensagem por Molina

Seg Ago 15, 2011 11:09
Sistemas de Equações
-
- ajude
por Amandatkm » Dom Mai 12, 2013 11:10
- 1 Respostas
- 2055 Exibições
- Última mensagem por Cleyson007

Dom Mai 12, 2013 14:22
Equações
-
- [logaritmo] Ajude-me, por favor.
por Cleyson007 » Sáb Mai 17, 2008 23:20
- 4 Respostas
- 12840 Exibições
- Última mensagem por Neperiano

Qui Jun 19, 2008 16:34
Logaritmos
-
- [determinantes] Por favor me ajude!!!
por Cleyson007 » Dom Jul 13, 2008 09:11
- 3 Respostas
- 7187 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 19:46
Matrizes e Determinantes
-
- [logaritmo] Ajude-me, por favor.
por Thayane Suzuki » Ter Ago 19, 2008 18:56
- 4 Respostas
- 6527 Exibições
- Última mensagem por admin

Sex Ago 22, 2008 00:38
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


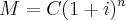
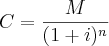
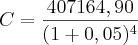
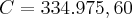
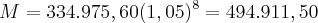



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.