 por Andreza » Ter Out 25, 2011 14:25
por Andreza » Ter Out 25, 2011 14:25
Considere os pontos do plano que verificam as seguintes condições:
y < x² + 1 ou y > 2.
O conjunto dos pontos do plano que não verificam essas condições determina qual região?
Y sendo maior que 2 posso substituí-lo por 3 ficando assim:
3 < x² + 1
x² + 1 > 3
x² > 3 – 1
x² > 2
x > ?2
Seria uma região limitada com infinitos pontos, ou ilimitada com infinitos pontos?
Estou em dúvida.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por LuizAquino » Ter Out 25, 2011 16:58
por LuizAquino » Ter Out 25, 2011 16:58
Andreza escreveu:Considere os pontos do plano que verificam as seguintes condições:
y < x² + 1 ou y > 2.
O conjunto dos pontos do plano que não verificam essas condições determina qual região?
Os pontos atendem a condição:
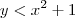
ou
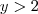
Note que a negação lógica disso seria:
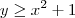
e
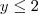
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função e conjunto de pontos
por Andreza » Sáb Nov 12, 2011 10:07
- 1 Respostas
- 1339 Exibições
- Última mensagem por nietzsche

Sáb Nov 12, 2011 15:21
Funções
-
- Circunferência, conjunto de pontos representados geometricam
 por elisamaria » Seg Jul 06, 2015 20:13
por elisamaria » Seg Jul 06, 2015 20:13
- 1 Respostas
- 1569 Exibições
- Última mensagem por nakagumahissao

Qua Ago 19, 2015 15:36
Geometria Analítica
-
- [Geometria Analítica] Área formada por pontos no plano
por acorreia » Ter Mai 08, 2012 18:05
- 1 Respostas
- 1797 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 20:36
Geometria Analítica
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2471 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5367 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


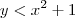 ou
ou 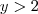
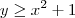 e
e 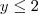


 .
.



