Uma urna contém 5 bolas amarelas numeradas de 1 a 5 e 8 bolas brancas numeradas de 1 a 8.
Um experimento consiste em retirar sucessivamente, sem repor a bola retirada, 7 bolas desta urna.
Estamos interessados na probabilidade de que não existam nem menos e nem mais do que 1 bola amarela entre as bolas extraídas.
(a) Defina o espaço amostral do experimento, por meio de uma propriedade.
(RESPOSTA) - Dentro dessa urna que é o nosso conjunto universo, temos dois subconjuntos que é:
B= formado por bolas brancas
C= formado por bolas amarelas
Podemos perceber que as bolas mesmo sendo da mesma cor são diferentes, pois todas são numeradas. Vamos representar o experimento por x. Este representa a sequência de bolas retiradas que são 7.
x= 1º bola, 2º bola, 3º bola, 4º bola, 5º bola, 6º bola e 7º bola.
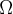={x
U / x (B
C)}(b) defina o evento A em questão, por meio de uma propriedade.
(RESPOSTA) - O evento A ocorre quando quando dentre as 7 bolas extraídas há uma bola amarela.
A={x
U / x tenha 6 elementos de B}a minha maior dúvida é se as minhas colocações sobre as propriedades estão corretas, por exemplo: eu poderia definir o evento A da forma que eu defini escrevendo.
desde já agradeço a atenção!!
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.