 por Aliiine » Seg Out 24, 2011 11:12
por Aliiine » Seg Out 24, 2011 11:12
1)Sete lugares,dispostos lado a lado e vão sortear entre 7 pessoas,3 homens e 4 mulheres.Qual a probabilidades de as mulheres sentarem juntas?!
tentei fazer por quantas possibilitadades total
7x6x5x4x3x2x1 = 5040
Depois fui tentar descobrir as possibilidades das mulheres sentarem juntas
1 X 1 X 1 X 1 X 3 X 2 X1 X P4
M M M M
Enfim ta dando errado (resposta 4/35)
2) QUAL A PROBABILIDADE DE,JOGANDO DOI DADOS A SOMA DOS RESULTADOS SER 10 ?!
CADA DADO TEM 6 FACES,ENTAO PARA OS DOIS DADOS VOU TER 12 FACES,MAS SÃO 36 POSSIBILIDADES,NÉ?!
PARA A SOMA DAR 10 SÓ PODE SER 5+5 OU 6+4
NO PRIMEIRO DADO POSSO TIRAR 3 JA NO SEGUNDO 2 OU NO PRIMEIRO 3 E NO SEGUNDO 3
NO FIM DARIA 6+9=14 ,
(RESPOSTA 1/12)
-
Aliiine
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 24, 2011 10:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por jose henrique » Seg Out 24, 2011 22:47
por jose henrique » Seg Out 24, 2011 22:47
O meu modo de entender a primeira questão resulta em uma permutação com elementos repetidos, pois nada impede que representemos mulheres com a letra M e homens com a letra H correto? e neste caso teríamos um espaço amostral com 35 elementos. Agora consideremos as quatros mulheres como um grupo só, pois só nos interessa quando elas estiverem juntas. Agora teríamos um arranjo.
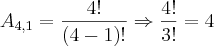
.Então como:
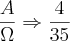
.
na segunda questão, temos como um espaço amostral o lançamento de dois dados, sendo representado pela letra "a" no primeiro lançamento e com a letra "b" para o segundo lançamento. o evento em questão pede que a+b=10
A={(5,5), (6,4), (4,6)}
n(A)=3
e que como vc mencionou que n(
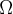
)=36
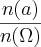
=
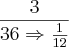
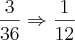
.
espero que tenha esclarecido suas dúvidas e que caso eu tenha aplicado alguma fórmula errada.Espero que algum professor possa esclarecer.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas
 por Adriana Barbosa » Seg Jun 01, 2009 11:01
por Adriana Barbosa » Seg Jun 01, 2009 11:01
- 1 Respostas
- 1723 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 07:00
Funções
-
- duvidas e + duvidas
por sukita » Ter Out 05, 2010 22:22
- 1 Respostas
- 1675 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 22:31
Progressões
-
- Duvidas
 por Paulo A G » Qua Jan 26, 2011 14:45
por Paulo A G » Qua Jan 26, 2011 14:45
- 1 Respostas
- 3003 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:09
Pedidos de Materiais
-
- 2 dúvidas
por analuiza » Qui Fev 17, 2011 23:14
- 1 Respostas
- 2723 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:33
Trigonometria
-
- Dúvidas ....
por vanessa134 » Seg Out 17, 2011 01:06
- 0 Respostas
- 1512 Exibições
- Última mensagem por vanessa134

Seg Out 17, 2011 01:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


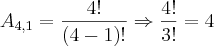 .Então como:
.Então como: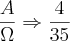 .
.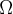 )=36
)=36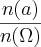 =
= 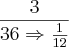
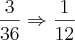 .
.





