Tem 7 maravilhas do mundo antigo e 7 maravilhas do mundo moderno e nenhuma pertence a ambos os conjuntos.Supondo que se escolham ,aleatoriamente,duas entre essa 14 maravilhas.Determine a probabilidade de ambos estarem em um mesmo grupo.(resposta 6/13)
EU TENHO 7/14 PARA SORTEAR 1 DO MESMO GRUPO
PARA SORTEAR DUAS DO MESMO GRUPO, 7/14 x 6/13 = 42/182=21/91=3/13=ERRADO U.U


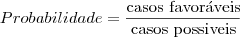 ,
,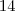 maravilhas.
maravilhas. restantes de seu respectivo grupo.
restantes de seu respectivo grupo.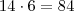
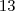 maravilhas restantes.
maravilhas restantes.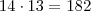
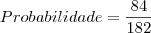
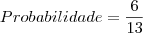
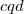
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.