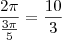por rodsales » Dom Abr 26, 2009 14:33
por rodsales » Dom Abr 26, 2009 14:33
A medida do ângulo externo de um polígono regular é 3Pi/5 rad. Quantos lados tem esse polígono?
obs: pensei de todas as maneiras mas não consegui visualizar como fazer, como tenho que estudar sozinho e como não faço cursinho, espero que vcs tenham paciência com minhas dúvidas.
Grato,
Aguardo Respostas...
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por admin » Dom Abr 26, 2009 15:15
por admin » Dom Abr 26, 2009 15:15
Olá
rodsales!
Primeiro certifique-se de identificar corretamente o ângulo externo, eles são suplementares adjacentes aos respectivos ângulos internos, veja na figura:
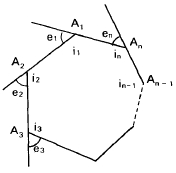
- angulo_externo.jpg (9.02 KiB) Exibido 4892 vezes
Você precisará utilizar que a soma dos ângulos externos de um polígono convexo é:

Tente continuar considerando que a soma dos ângulos externos é:
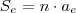
Nota: eu fiz e não obtive

inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Marcampucio » Dom Abr 26, 2009 15:24
por Marcampucio » Dom Abr 26, 2009 15:24

O ângulo externo de um polígono
regular é igual ao seu ângulo interno. A medida do ângulo é dada por
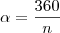
em graus.
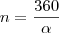
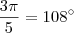
que não é ângulo de polígono regular. Veja:
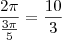
logo há um êrro no seu dado...
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por admin » Dom Abr 26, 2009 15:38
por admin » Dom Abr 26, 2009 15:38
Marcampucio escreveu:O ângulo externo de um polígono regular é igual ao seu ângulo interno.
Olá
Marcampucio!
Como o ângulo externo é suplementar ao interno, eles não seriam iguais apenas para o quadrado?
Contra-exemplos:
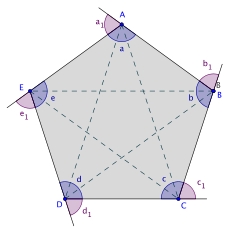
- pentagono_regular.jpg (19.94 KiB) Exibido 6250 vezes
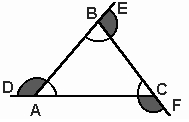
- triangulo.jpg (6.8 KiB) Exibido 6238 vezes
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Marcampucio » Dom Abr 26, 2009 15:54
por Marcampucio » Dom Abr 26, 2009 15:54
Olá fabiosouza,
eu dizia ângulo interno=ângulo central

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por rodsales » Dom Abr 26, 2009 21:04
por rodsales » Dom Abr 26, 2009 21:04
Bem, estou estudando pelo livro "Curso Prático de Matemática", de Paulo Bucchi. É um exercício da pg 348, 24. Quem puder dêem uma olhada. Mesmo assim fico muito grato as respostas de vcs.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




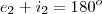




 por
por 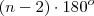 que por sua vez também aceita outra dedução...
que por sua vez também aceita outra dedução... 
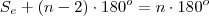
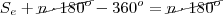
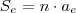
 inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.
inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.

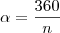 em graus.
em graus.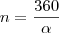
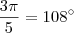 que não é ângulo de polígono regular. Veja:
que não é ângulo de polígono regular. Veja: