Por gentileza, alguém pode me ajudar nessa resolução:
Demonstre que:
1.2+2.3+3.4+...+n(n+1) = n.(n+1).(n+2)/3 , para n natural
(Dica) estude demonstrações por indução finita.



silvia fillet escreveu:Por gentileza, alguém pode me ajudar nessa resolução:
Demonstre que:
1.2+2.3+3.4+...+n(n+1) = n.(n+1).(n+2)/3 , para n natural
(Dica) estude demonstrações por indução finita.

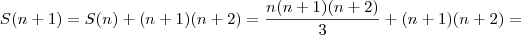



MarceloFantini escreveu:Não entendi muito bem o que você fez para a indução, a demonstração para o primeiro caso está certa. Aqui vai:
Que prova a veracidade.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante