por maria cleide » Qui Out 13, 2011 11:33
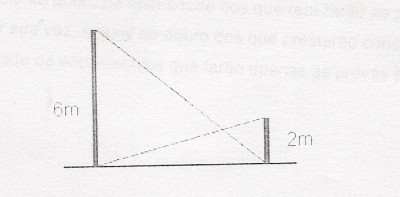
Em uma exposição artística um escultor apresentou sua obra prima, intitulanda "as torres vizinhas". Repare que a mesma consta de duas hastes paralelas de ferro fundidas perpendicularmente em uma mesma base e escoradas por dois cabos de aço retilíneos, como mostra a figura abaixo. As alturas das hastes medem, respectivamente, 6 metros e 2 metros. Desprezando-se a espesura dos cabos, determine a distância do ponto de interseção dos cabos à base da escultura.
Eu consegui encontra dois triângulos cujas bases são 6 e 2, mas não consegui desenvolver isto.
- Anexos
-
-
maria cleide
- Usuário Parceiro
-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
por maria cleide » Sex Out 14, 2011 22:43
Por favor, me ajudem.
Obrigada M.C.
-
maria cleide
- Usuário Parceiro
-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
