[Sistemas Lineares] Precisão do Método de Gauss-Seidel

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Sistemas Lineares] Precisão do Método de Gauss-Seidel

Regras do fórum
Responder

[Sistemas Lineares] Precisão do Método de Gauss-Seidel

Mensagempor VFernandes » Qui Out 06, 2011 13:50

Caros amigos, primeiramente peço desculpas se o assunto foge um pouco do tema, mas foi a seção mais adequada que encontrei.
Tenho o seguinte problema em minhas mãos:
\begin{pmatrix} 4 & -1 & 0 \\ -2 & 3 & -1 \\ -1 & -3 & 5 \end{pmatrix} \begin{pmatrix} {x}_{1}} \\ {x}_{2}} \\ {x}_{3}} \end{pmatrix} = \begin{pmatrix} 2\\ 0 \\ 1 \end{pmatrix}
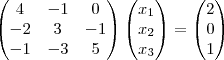
Calcule uma iteração por Gauss-Seidel, partindo de = (0,0,0) e estime quantas iterações são necessárias para que se atinja a precisão \epsilon = 0.0001
Bom, vamos lá:

{{x}_{1}}^{1} = \frac{1}{4}(2-(-1)\times0-0\times0)) = 0,5
{{x}_{2}}^{1} = \frac{1}{3}(0-(-2)\times0,5-(-1)\times0)) = 0,33
{{x}_{3}}^{1} = \frac{1}{5}(1-(-1)\times0,5-(-3)\times0,33)) = 0,5

\beta_1 = \frac{1}{4}(1+0) = 0,25
\beta_ = \frac{1}{3}(2\times0,25+1) = 0,5
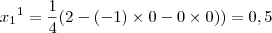
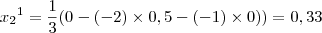
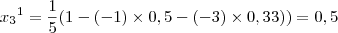
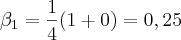
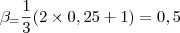
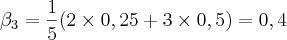\beta_3 = \frac{1}{5}(2\times0,25+3\times0,5) = 0,4 portanto,
M = 0.5 (maior dos betas)
Até aqui, sem problemas, a questão vem agora:
Sabemos que:
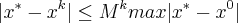|x^*-x^k|\leq M^k max|x^*-x^0| portanto,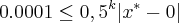
0.0001\leq 0,5^k |x^*-0|
o que não nos ajuda em muito, pois não sabemos x* (valor exato de x)
Alguma alma caridosa saberia como lidar com isso? Será que temos que delimitar um intervalo onde está contida a solução do sistema?
VFernandes
Novo Usuário
Novo Usuário
 
Mensagens: 6
Registrado em: Sex Mar 04, 2011 16:47
Formação Escolar: GRADUAÇÃO
Área/Curso: Eng. Elétrica
Andamento: cursando
Voltar ao topo
Responder

Voltar para Sistemas de Equações

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 10:38

Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:

Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?

Grata.

Assunto: Conjunto dos números racionais.
Autor: MarceloFantini - Sex Fev 18, 2011 12:27

x^2 = \frac{x}{3}

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 12:55

também pensei que fosse assim, mas a resposta é \frac{1}{3}.

Obrigada Fantini.

Assunto: Conjunto dos números racionais.
Autor: MarceloFantini - Sex Fev 18, 2011 13:01

x^2 = \frac{x}{3} \Rightarrow x^2 - \frac{x}{3} = 0 \Rightarrow x \left(x - \frac{1}{3} \right) = 0

Como x \neq 0:

x - \frac{1}{3} = 0 \Rightarrow x = \frac{1}{3}

O que você fez?

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 16:17

eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.

Obrigada.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum