 por vanessafey » Seg Set 12, 2011 15:17
por vanessafey » Seg Set 12, 2011 15:17
Não consegui entender a lógica das Matrizes Inversas...
Exemplo:
Tenho a matriz

Como calcular
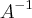
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessafey » Seg Set 12, 2011 16:53
por vanessafey » Seg Set 12, 2011 16:53
Vou postar como fiz... não sei se corretamente...
Solução:
sabendo que o

e também a matriz adjunta

Então
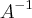
calculando a matriz inversa usando a matriz adjunta, encontrei

O que não está de acordo com o gabarito!!! Alguém pode me responder onde estou errando?
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessafey » Qua Set 21, 2011 20:45
por vanessafey » Qua Set 21, 2011 20:45
Oi, alguém pode me dizer se está correta esta questão? Não recebi nenhuma resposta...
Obrigada

-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qua Set 21, 2011 21:40
por MarceloFantini » Qua Set 21, 2011 21:40
Eu conheço o jeito mais "bruto" de se calcular a matriz inversa, que é você colocar uma matriz genérica

tal que

. Deve existir algum algoritmo mais fácil.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Set 21, 2011 23:23
por LuizAquino » Qua Set 21, 2011 23:23
vanessafey escreveu:Tenho a matriz

vanessafey escreveu:sabendo que o det(A)=45
Ok.
vanessafey escreveu:e também a matriz adjunta

Ok.
vanessafey escreveu:Então
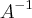
calculando a matriz inversa usando a matriz adjunta, encontrei

Ok. Faltou apenas simplificar as frações -6/45 (que dá -2/15) e 21/45 (que dá 7/15).
MarceloFantini escreveu:Eu conheço o jeito mais "bruto" de se calcular a matriz inversa, que é você colocar uma matriz genérica

tal que

. Deve existir algum algoritmo mais fácil.
Sim, há uma algoritmo mais simplificado. Vide:
Matriz Inversa - Conteúdos de Álgebra Linearhttp://www.igm.mat.br/aplicativos/index ... onteudosal
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4497 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
-
- Matriz - Inversa ou não?
por Bruhh » Seg Mar 08, 2010 16:31
- 7 Respostas
- 16144 Exibições
- Última mensagem por Neperiano

Qui Mar 11, 2010 15:50
Conversão de Unidades
-
- Matriz Inversa
por Claudin » Qui Set 15, 2011 17:44
- 11 Respostas
- 5305 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 18:51
Matrizes e Determinantes
-
- Inversa da Matriz
por brunojorge29 » Seg Out 10, 2011 09:48
- 4 Respostas
- 2931 Exibições
- Última mensagem por brunojorge29

Qua Out 12, 2011 17:30
Matrizes e Determinantes
-
- Matriz inversa
por ViniRFB » Sex Mar 09, 2012 14:33
- 1 Respostas
- 1405 Exibições
- Última mensagem por ViniRFB

Sex Mar 09, 2012 14:49
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

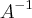


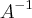

 e também a matriz adjunta
e também a matriz adjunta 
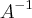 calculando a matriz inversa usando a matriz adjunta, encontrei
calculando a matriz inversa usando a matriz adjunta, encontrei



 tal que
tal que  . Deve existir algum algoritmo mais fácil.
. Deve existir algum algoritmo mais fácil.

calculando a matriz inversa usando a matriz adjunta, encontrei
tal que
. Deve existir algum algoritmo mais fácil.



 , avisa que eu resolvo.
, avisa que eu resolvo.

