 por Anne2011 » Sex Set 16, 2011 23:17
por Anne2011 » Sex Set 16, 2011 23:17
E essa agora?
![\int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1 \int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1](/latexrender/pictures/bb89ab141a6dea0a3804327660af9aeb.png)
Fiz a primeira vez sem dividir a integral em duas, e depois separei mas não deu certo...
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 23:28
por MarceloFantini » Sex Set 16, 2011 23:28
Qual foi o seu desenvolvimento? A substituição está certa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sáb Set 17, 2011 17:28
por MarceloFantini » Sáb Set 17, 2011 17:28
Você acertou a substituição e a derivada, mas você
NÃO DEVE isolar o
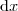
! E não existe essa separação de integral, isto é um erro
gravíssimo! Aqui está como você deve fazer:
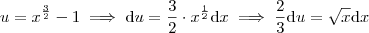
Fazendo a substituição na integral:
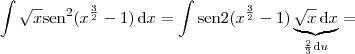
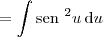
Agora use que
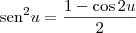
e a integral sairá facilmente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida (por substituição)
por Anne2011 » Sex Set 16, 2011 21:00
- 5 Respostas
- 3344 Exibições
- Última mensagem por Anne2011

Sex Set 16, 2011 21:47
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Qua Out 03, 2012 13:24
- 2 Respostas
- 2352 Exibições
- Última mensagem por fabriel

Qua Out 03, 2012 15:15
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Seg Nov 26, 2012 00:03
- 4 Respostas
- 3257 Exibições
- Última mensagem por fabriel

Ter Nov 27, 2012 01:23
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Indefinida] Método por Substituição
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- 3 Respostas
- 3012 Exibições
- Última mensagem por e8group

Dom Mar 03, 2013 18:15
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Substituição Trigonométrica / Indefinida
por Elvis » Dom Out 18, 2015 13:14
- 1 Respostas
- 2441 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1 \int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1](/latexrender/pictures/bb89ab141a6dea0a3804327660af9aeb.png)

![\int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1 \int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1](/latexrender/pictures/bb89ab141a6dea0a3804327660af9aeb.png)



![\int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx \int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx](/latexrender/pictures/5169edfda878fc9965123905c2b64e13.png)
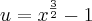
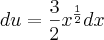
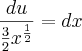
![\int_{}^{}\sqrt[]{x}dx \int_{}^{}{sen}^{2}({x}^{\frac{3}{2}}-1)dx \int_{}^{}\sqrt[]{x}dx \int_{}^{}{sen}^{2}({x}^{\frac{3}{2}}-1)dx](/latexrender/pictures/b4c4d9a14dbebed707963a75e2f14e4c.png)
![\int_{}^{}\sqrt[]{x}\frac{du}{\frac{3}{2}{x}^{\frac{1}{2}}} \int_{}^{}{sen}^{2}u\frac{du}{\frac{3}{2}{x}^{\frac{1}{2}}} \int_{}^{}\sqrt[]{x}\frac{du}{\frac{3}{2}{x}^{\frac{1}{2}}} \int_{}^{}{sen}^{2}u\frac{du}{\frac{3}{2}{x}^{\frac{1}{2}}}](/latexrender/pictures/dd09bc16f5a3c65040649edb263e8cb4.png)
![\int_{}^{}\sqrt[]{x}\frac{du}{\frac{3\sqrt[]{x}}{2}} \int_{}^{}{sen}^{2}u\frac{du}{\frac{3\sqrt[]{x}}{2}} \int_{}^{}\sqrt[]{x}\frac{du}{\frac{3\sqrt[]{x}}{2}} \int_{}^{}{sen}^{2}u\frac{du}{\frac{3\sqrt[]{x}}{2}}](/latexrender/pictures/c0121886b9f2f8b544402e77e6759eee.png)

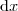 ! E não existe essa separação de integral, isto é um erro gravíssimo! Aqui está como você deve fazer:
! E não existe essa separação de integral, isto é um erro gravíssimo! Aqui está como você deve fazer: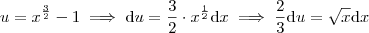
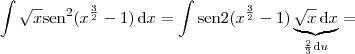
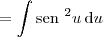
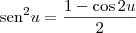 e a integral sairá facilmente.
e a integral sairá facilmente.
