Claudin escreveu:Mas mesmo realizando operações elementares no escalonamento por Gauss Jordan, alteraria o determinante:
Sim. Algumas operações poderiam alterar o determinante. Eu recomendo que você leia o capítulo sobre determinantes do livro de Reginaldo Santos (UFMG). Esse livro está disponível na página dele:
Matrizes, Vetores e Geometria Analíticahttp://www.mat.ufmg.br/~regi/livros.htmlClaudin escreveu:Então foi este o meu erro, prefiro fazer por cofator mesmo.
Calcular um determinante por cofator é a pior estratégia numérica que você pode usar.
Apenas como exemplo, considere o trabalho de calcular o determinante de uma matriz 20 por 20.
Para esse cálculo por cofatores seria necessário calcular o determinante de 20 matrizes de ordem 19 por 19. Para cada uma dessas matrizes, seria necessário calcular o determinante de 19 matrizes de ordem 18 por 18. Continuando essa ideia, percebemos que iríamos precisar calcular 20! multiplicações (não estou contando nem as somas!).
Pois bem, um computador pessoal atualmente faz por volta de
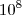
multiplicações por segundo. Por outro lado, sabemos que 20! é aproximadamente
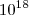
. Sendo assim, esse computador levaria
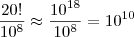
segundos para fazer 20! multiplicações. Mas
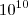
segundos correspondem a aproximadamente 317 anos!
Agora pense no seguinte: quantas multiplicações por segundo um ser humano consegue fazer? Provavelmente ele levaria a vida toda e não conseguiria calcular o determinante de uma matriz 20 por 20 não trivial utilizando o método por cofator.


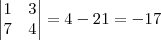
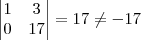


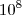 multiplicações por segundo. Por outro lado, sabemos que 20! é aproximadamente
multiplicações por segundo. Por outro lado, sabemos que 20! é aproximadamente 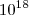 . Sendo assim, esse computador levaria
. Sendo assim, esse computador levaria 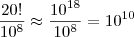 segundos para fazer 20! multiplicações. Mas
segundos para fazer 20! multiplicações. Mas 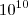 segundos correspondem a aproximadamente 317 anos!
segundos correspondem a aproximadamente 317 anos! .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
