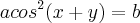
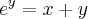
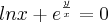


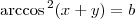 pode ser vista como
pode ser vista como  .
.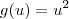
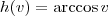
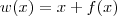
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
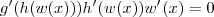
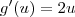
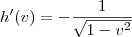
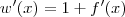
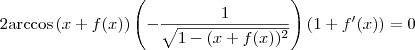
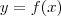 e
e 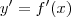 , ficamos com
, ficamos com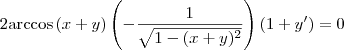

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.