 por moyses » Sex Set 09, 2011 00:24
por moyses » Sex Set 09, 2011 00:24
oi pessoal mais um limites no infinito! quiria saber como usar tecnicas propriedades para tirar esse exercicio
![\lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/fff8d9e41a8b08265504117c148b3367.png)
a pergunta é a seguinte : um amigo aqui do forum o luiz me encinou que da para usar propriedades de potenciação para tirar tipos e indeterminaçoes como

o problema é que esse exercicio cai numa indeterminação de

tem como usar as propriedades de potenciação nesse exercicio para tirar a indeterminação como esse que eu acabei de apresentar a vocês por favor me respondam:
Ps:eu sei propriedade mais com raiz eu nunca fiz, se não for incomodo por favor me passe um link confiavel que tenha funçoes trigonometricas , logaritmos de base E, e tabem limites fundamentais trigonometricos e limites fundamentais esponencial se não for encomodo! desde já agradeço a atenção de todos valew pessoal



-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por Aliocha Karamazov » Sex Set 09, 2011 01:13
por Aliocha Karamazov » Sex Set 09, 2011 01:13
Nesse casos em que aparecem raízes, multiplique pelo conjugado. Fica assim:
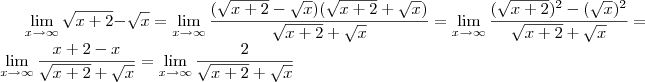
Agora, fica mais fácil. Tente terminar. Se tiver dúvida, poste que eu coloco o resto da resolução.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por moyses » Sex Set 09, 2011 09:53
por moyses » Sex Set 09, 2011 09:53
ahh sim eu entendi o que você Aliocha Karamazov fez, vamos lá ! eu sabia que dava para multiplicar pelo conjugado , mais eu não sabia como. Deixa eu entender!
![\lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/80d46f702b506210024f6cb24682ba2f.png)
ai você pegou e multiplicou em cima e embaixa pro um mesmo valor só que o conjugado desse valor correto? ai quando você multiplicou esse por
![\frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}} \frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/f79279af1f4011f2e49ee9b9b6a9df44.png)
que não altera a fração , pois resultara no fração equivalente certo? ai você pegou e fez isso
![\lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/dcc93ff5392a1046de16813b89e7e313.png)
que resulta nisso

:
![\lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/c00c3bbaa8abd0ffc94223792d8f3b9a.png)
depois fica assim ne?
![\lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/1ad1bc19ad8c1c273a293be2128e94dd.png)
=
![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/b4819d27bdeb6650e48231cca6582860.png)
agora se eu resolver fica assim:
![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}}](/latexrender/pictures/bc479ca20d5a363aeda0d63bcb3d7ad1.png)
=
![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}}](/latexrender/pictures/34192202a168afdfc191d2eb4b928027.png)
=
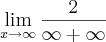
=
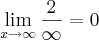
esse é eo resultado, se for se esclareça uma duvida? por qualquer numero não nulo sobre infinito vira 0? desde já valew pela ajuda ai no exercicio pessoal valeww




-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por MarceloFantini » Sex Set 09, 2011 16:18
por MarceloFantini » Sex Set 09, 2011 16:18
Infinito não é número, então tome cuidado com este abuso de notação que você fez (e que está errado pois manteve o limite). Nunca escreva isso em uma prova. E sim, sempre que temos
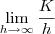
, onde K é uma constante, o limite será zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por moyses » Sáb Set 10, 2011 11:25
por moyses » Sáb Set 10, 2011 11:25
como assim o infinito não é um numero!? mais o infinito não é numero que nunca para de crescer? por favor explique isso MarceloFantini? e exclique isso tabem por que k sobre infinito vira 0? so por curiosidade ? e que eu gosto muito de matemática!

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Set 10, 2011 19:29
por MarceloFantini » Sáb Set 10, 2011 19:29
Infinito não é número, infinito é um conceito. Usamos ele para denotar eventos prolongados por muito tempo, grandes quantidades relativas às que temos, etc. Não existe número que não pára de crescer, pois se é número então ele é finito. Sobre o limite, basta notar que
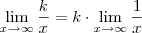
que vai para zero, e portanto o limite inteiro vai para zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por moyses » Dom Set 11, 2011 09:04
por moyses » Dom Set 11, 2011 09:04
valeww cara pela excelente explicação! então o infinito é só um conceito, mais não é interessante ? olha só que interessante
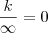
e
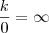
sera que eu estou certo? o infinito é um conceito de indeterminação ? mais quando dividimos k por 0 vai ser igual a +- infinito, é claro se os limites laterais forem iguais ai sim o limite que você fez ali no ponto esta correto!. quando dividimos k por 0 vai ser uma indeterminação , tentando entender sua explicação quando dividimos k por qualquer numero tentamos fazer que o denominador multiplicado por x numero , chegue ao k no numerador e o resultado é o numero que vc multiplica e chega no valor do denominador ! certo? mais qunado k e divido por 0 e k é dirente de 0 seja ele negativo ou positivo, então quantas vezes eu devo multiplicar 0 para chegar em k? não tem como pois 0 vezes qualquer coisa é sempre 0, por isso vai dar infinito pois eu ficarei infinitamente m,ultiplicando 0 para chegar a k é isso? e por isso o resultado via ser infinito?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Set 11, 2011 12:37
por MarceloFantini » Dom Set 11, 2011 12:37
Desculpe, não entendi seu texto. Pode tentar ser um pouco mais claro? E o conceito de infinito é muito interessante sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por moyses » Seg Set 12, 2011 09:55
por moyses » Seg Set 12, 2011 09:55
decupa pelo enorme texto rsrsr

! eu só to querendo dizer que é interresante que uma constante sobre o infinito vira 0 o limite todo! eu só quiria que você explicasse por que isso acontece? e tabem por que uma constante sobre 0 vira infinito e só isso?valew pela ajuda valew mesmo acho que eu quero ser professor de matemática tabem rsrsrs! mais não de portugues e nem sei escrever direito rsrsr

!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Set 12, 2011 12:18
por LuizAquino » Seg Set 12, 2011 12:18
Moyses,
Nas
vídeo-aulas "05. Cálculo I - Limites Infinitos" e "06. Cálculo I - Limites no Infinito" é explicado a ideia por trás desses resultados. Eu recomendo que você assista.
Além disso, vale chamar sua atenção para uma questão de notação.
Quando você lê em um texto de Cálculo algo do tipo

, isso
não quer dizer a "
divisão entre a constante k e o infinito". Na verdade, quando você lê essa notação você tem que entender o seguinte: temos um limite do tipo
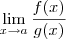
no qual sabemos que
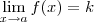
e
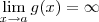
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Indeterminação (infinito-infinito)
por Marcampucio » Seg Mar 16, 2009 00:16
- 4 Respostas
- 19665 Exibições
- Última mensagem por stuart clark

Seg Mai 30, 2011 06:21
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Indeterminação do tipo 0X+infinito
por Pollyanna Moraes » Sáb Abr 28, 2012 15:04
- 1 Respostas
- 2956 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 09:05
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3536 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação - Limite
por Paloma » Ter Mar 16, 2010 21:06
- 10 Respostas
- 9738 Exibições
- Última mensagem por Paloma

Sáb Mar 20, 2010 13:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Indeterminação
 por Aliocha Karamazov » Sex Nov 25, 2011 00:28
por Aliocha Karamazov » Sex Nov 25, 2011 00:28
- 2 Respostas
- 1956 Exibições
- Última mensagem por Aliocha Karamazov

Sex Nov 25, 2011 21:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}=\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/fff8d9e41a8b08265504117c148b3367.png) a pergunta é a seguinte : um amigo aqui do forum o luiz me encinou que da para usar propriedades de potenciação para tirar tipos e indeterminaçoes como
a pergunta é a seguinte : um amigo aqui do forum o luiz me encinou que da para usar propriedades de potenciação para tirar tipos e indeterminaçoes como o problema é que esse exercicio cai numa indeterminação de
o problema é que esse exercicio cai numa indeterminação de  tem como usar as propriedades de potenciação nesse exercicio para tirar a indeterminação como esse que eu acabei de apresentar a vocês por favor me respondam:
tem como usar as propriedades de potenciação nesse exercicio para tirar a indeterminação como esse que eu acabei de apresentar a vocês por favor me respondam:



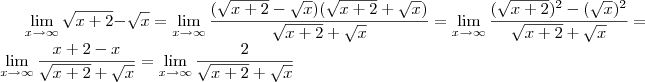
![\lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x} \lim_{x\rightarrow\infty}\sqrt[]{x+2}-\sqrt[]{x}](/latexrender/pictures/80d46f702b506210024f6cb24682ba2f.png) ai você pegou e multiplicou em cima e embaixa pro um mesmo valor só que o conjugado desse valor correto? ai quando você multiplicou esse por
ai você pegou e multiplicou em cima e embaixa pro um mesmo valor só que o conjugado desse valor correto? ai quando você multiplicou esse por ![\frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}} \frac{\sqrt[]{x+2}+\sqrt[]{x}}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/f79279af1f4011f2e49ee9b9b6a9df44.png) que não altera a fração , pois resultara no fração equivalente certo? ai você pegou e fez isso
que não altera a fração , pois resultara no fração equivalente certo? ai você pegou e fez isso ![\lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{\left(\sqrt[]{x+2}-\sqrt[]{x} \right)\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/dcc93ff5392a1046de16813b89e7e313.png) que resulta nisso
que resulta nisso  :
: ![\lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)} \lim_{x\rightarrow\infty}\frac{{\sqrt[]{x+2}}^{2}-{\sqrt[]{x}}^{2}}{1\left(\sqrt[]{x+2}+\sqrt[]{x} \right)}](/latexrender/pictures/c00c3bbaa8abd0ffc94223792d8f3b9a.png) depois fica assim ne?
depois fica assim ne? ![\lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{x+2-x}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/1ad1bc19ad8c1c273a293be2128e94dd.png) =
= ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{x+2}+\sqrt[]{x}}](/latexrender/pictures/b4819d27bdeb6650e48231cca6582860.png) agora se eu resolver fica assim:
agora se eu resolver fica assim: ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty+2}+\sqrt[]{\infty}}](/latexrender/pictures/bc479ca20d5a363aeda0d63bcb3d7ad1.png) =
= ![\lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}} \lim_{x\rightarrow\infty}\frac{2}{\sqrt[]{\infty}+\sqrt[]{\infty}}](/latexrender/pictures/34192202a168afdfc191d2eb4b928027.png) =
=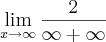 =
= 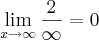 esse é eo resultado, se for se esclareça uma duvida? por qualquer numero não nulo sobre infinito vira 0? desde já valew pela ajuda ai no exercicio pessoal valeww
esse é eo resultado, se for se esclareça uma duvida? por qualquer numero não nulo sobre infinito vira 0? desde já valew pela ajuda ai no exercicio pessoal valeww 

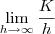 , onde K é uma constante, o limite será zero.
, onde K é uma constante, o limite será zero.

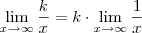 que vai para zero, e portanto o limite inteiro vai para zero.
que vai para zero, e portanto o limite inteiro vai para zero.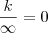 e
e 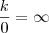 sera que eu estou certo? o infinito é um conceito de indeterminação ? mais quando dividimos k por 0 vai ser igual a +- infinito, é claro se os limites laterais forem iguais ai sim o limite que você fez ali no ponto esta correto!. quando dividimos k por 0 vai ser uma indeterminação , tentando entender sua explicação quando dividimos k por qualquer numero tentamos fazer que o denominador multiplicado por x numero , chegue ao k no numerador e o resultado é o numero que vc multiplica e chega no valor do denominador ! certo? mais qunado k e divido por 0 e k é dirente de 0 seja ele negativo ou positivo, então quantas vezes eu devo multiplicar 0 para chegar em k? não tem como pois 0 vezes qualquer coisa é sempre 0, por isso vai dar infinito pois eu ficarei infinitamente m,ultiplicando 0 para chegar a k é isso? e por isso o resultado via ser infinito?
sera que eu estou certo? o infinito é um conceito de indeterminação ? mais quando dividimos k por 0 vai ser igual a +- infinito, é claro se os limites laterais forem iguais ai sim o limite que você fez ali no ponto esta correto!. quando dividimos k por 0 vai ser uma indeterminação , tentando entender sua explicação quando dividimos k por qualquer numero tentamos fazer que o denominador multiplicado por x numero , chegue ao k no numerador e o resultado é o numero que vc multiplica e chega no valor do denominador ! certo? mais qunado k e divido por 0 e k é dirente de 0 seja ele negativo ou positivo, então quantas vezes eu devo multiplicar 0 para chegar em k? não tem como pois 0 vezes qualquer coisa é sempre 0, por isso vai dar infinito pois eu ficarei infinitamente m,ultiplicando 0 para chegar a k é isso? e por isso o resultado via ser infinito? , isso
, isso 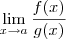 no qual sabemos que
no qual sabemos que 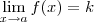 e
e 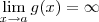 .
.


