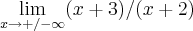
Para achar a assintota horizontal é achar o limite certo?
Nesse caso, meu limite deu +
 ... isso quer dizer que não existem assintotas horizontais?
... isso quer dizer que não existem assintotas horizontais?
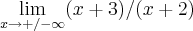
 ... isso quer dizer que não existem assintotas horizontais?
... isso quer dizer que não existem assintotas horizontais?

isanobile escreveu:Para achar a assintota horizontal é achar o limite certo?
isanobile escreveu:Fiz novamente pela regra do polinomio, e deu 1...
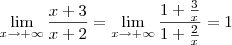
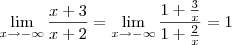
isanobile escreveu:Quando eu uso essa "regra"? ( dividir numerador e denominador pelo x^ maior grau do denominador)? sempre que tiver que achar assintotas horizontais?
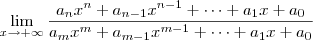
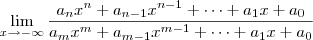
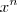 . Mas caso n < m, então você faz a divisão por
. Mas caso n < m, então você faz a divisão por 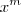 . Obviamente, se n = m tanta faz dividir por qualquer um deles.
. Obviamente, se n = m tanta faz dividir por qualquer um deles.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)