 por Sergio Batista Lima » Ter Ago 30, 2011 22:39
por Sergio Batista Lima » Ter Ago 30, 2011 22:39
Uma lista de preços de custo de produtos é fornecida ao funcionário de uma loja de conveniência. O gerente solicita que ele determine um número pelo qual todos os valores (referentes a preços de custo)da lista sejam multiplicados para obter o preço de venda de cada produto de forma que o lucro obtido com a venda corresponda a 40% do preço de venda. Que número (aproximado) é esse?
1,350; 1,540; 1,667; 1,750; 1,856.
-
Sergio Batista Lima
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Dom Ago 28, 2011 13:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Ter Ago 30, 2011 23:21
por LuizAquino » Ter Ago 30, 2011 23:21
Considere as seguintes incógnitas:
- C : preço de custo;
- V : preço de venda;
- L : lucro.
Dos dados do exercício, veja que devemos ter 40%V = L. Isso significa que 60%V = C.
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Sergio Batista Lima » Qua Ago 31, 2011 08:45
por Sergio Batista Lima » Qua Ago 31, 2011 08:45
Prezado, não consegui resolver. Favor me ajudar.
-
Sergio Batista Lima
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Dom Ago 28, 2011 13:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Ago 31, 2011 11:38
por LuizAquino » Qua Ago 31, 2011 11:38
Leia com atenção essa parte do enunciado do exercício:
(...) determine um número pelo qual todos os valores (referentes a preços de custo) da lista sejam multiplicados para obter o preço de venda de cada produto (...)Você deseja multiplicar um número por C de modo a obter V.
Ora, pelo que vimos antes sabemos que 60%V = C. Veja que isso é o mesmo que escrever
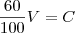
. Portanto, temos que
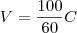
.
Veja se agora você consegue concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Sergio Batista Lima » Qua Ago 31, 2011 12:05
por Sergio Batista Lima » Qua Ago 31, 2011 12:05
Prezado. A resposta dá 1.667.
-
Sergio Batista Lima
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Dom Ago 28, 2011 13:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Ago 31, 2011 12:10
por LuizAquino » Qua Ago 31, 2011 12:10
Sergio Batista Lima escreveu:Prezado. A resposta dá 1.667.
Sim, é aproximadamente isso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10728 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9739 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3323 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4620 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6545 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



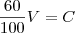 . Portanto, temos que
. Portanto, temos que 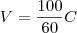 .
.