 por lucas7 » Ter Ago 30, 2011 21:39
por lucas7 » Ter Ago 30, 2011 21:39
Boa noite.
Medi o lado de um mesmo triângulo através de duas maneiras diferentes, e cheguei a dois resultados distintos(que acredito que sejam iguais).
![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png)
e
![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png)
Alguém pode me provar que ambas equações são iguais? Ou como fatorar
![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png)
para chegar em
![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png)
? Muito obrigado!
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Caradoc » Ter Ago 30, 2011 22:04
por Caradoc » Ter Ago 30, 2011 22:04
Sim, são quantidades iguais.
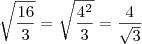
Daí racionalizando:
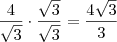
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por lucas7 » Ter Ago 30, 2011 22:09
por lucas7 » Ter Ago 30, 2011 22:09
Obrigado pela resposta! Outra pergunta:
![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png)
=
![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png)
certo? A partir desse ultimo numero, como vc racionalizaria a raíz quadrada fracionária? Obrigado novamente.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por lucas7 » Ter Ago 30, 2011 22:14
por lucas7 » Ter Ago 30, 2011 22:14
e uma ultima pergunta, desculpe, mas ajudaria terminar com minhas duvidas:
![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png)
é igual a
![\frac{4}{\sqrt[2]{3}} \frac{4}{\sqrt[2]{3}}](/latexrender/pictures/03d21149cdece26f80c18746cb99b5f7.png)
?
obrigado
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Caradoc » Ter Ago 30, 2011 22:30
por Caradoc » Ter Ago 30, 2011 22:30
Existe uma propriedade dos radicais que diz: "o radical de um quociente é igual ao quociente dos radicais"
Assim:
![\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](/latexrender/pictures/7a922c3446debb68c0d058dbbdbc1a74.png)
Daí que vem minha simplificação.
Por isso
![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png)
é igual a
![\frac{4}{\sqrt[2]{3}} \frac{4}{\sqrt[2]{3}}](/latexrender/pictures/03d21149cdece26f80c18746cb99b5f7.png)
.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por lucas7 » Qua Ago 31, 2011 15:18
por lucas7 » Qua Ago 31, 2011 15:18
Entendido. Agradecidíssimo!
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7465 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 6007 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2353 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17651 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2096 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png) e
e ![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png)
![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png) para chegar em
para chegar em ![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png) ? Muito obrigado!
? Muito obrigado!
![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png) e
e ![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png)
![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png) para chegar em
para chegar em ![\frac{4\sqrt[2]{3}}{3} \frac{4\sqrt[2]{3}}{3}](/latexrender/pictures/f6dc7d20d2076aef313ff5fe3fb54fbe.png) ? Muito obrigado!
? Muito obrigado!
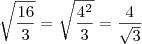
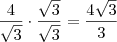

![\sqrt[2]{\frac{16}{3}} \sqrt[2]{\frac{16}{3}}](/latexrender/pictures/5ff93795ddbe52d22659ab0034984e94.png) =
= ![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png) certo? A partir desse ultimo numero, como vc racionalizaria a raíz quadrada fracionária? Obrigado novamente.
certo? A partir desse ultimo numero, como vc racionalizaria a raíz quadrada fracionária? Obrigado novamente.
![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png) é igual a
é igual a ![\frac{4}{\sqrt[2]{3}} \frac{4}{\sqrt[2]{3}}](/latexrender/pictures/03d21149cdece26f80c18746cb99b5f7.png) ?
?
![\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](/latexrender/pictures/7a922c3446debb68c0d058dbbdbc1a74.png)
![4\sqrt[2]{\frac{1}{3}} 4\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/484b0d312b9735eec832f6a18c5a6b3e.png) é igual a
é igual a ![\frac{4}{\sqrt[2]{3}} \frac{4}{\sqrt[2]{3}}](/latexrender/pictures/03d21149cdece26f80c18746cb99b5f7.png) .
.

