 por lucat28 » Ter Ago 30, 2011 19:32
por lucat28 » Ter Ago 30, 2011 19:32
Fala galera,
eu to com uma dificuldade muito grande em calcular área por integral,
a questão é a seguinte:
Determine a área limitada pela parábora y =
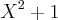
e pela reta y =
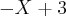
Gráfico :

A resposta é 4,5. Mas não conseguir encontrar de jeito nenhum a resposta certa.
o link da imagem do gráfico caso haja problema na de cima.
http://imageshack.us/photo/my-images/819/grfico2i.jpg/Agradeço a todos desde já

-
lucat28
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 16, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por LuizAquino » Ter Ago 30, 2011 22:08
por LuizAquino » Ter Ago 30, 2011 22:08
Primeiro, você precisa determinar a interseção entre a parábola e a reta.
Para isso, resolva a equação:
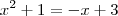
Você deve encontrar que as soluções são x = -2 e x = 1. Isso significa que para esses valores de x, o valor de y tanto para a parábola quanto para a reta será o mesmo.
Após fazer o esboço dos gráficos, você percebe que no intervalo [-2, 1] a reta está "acima" da parábola. Isto é, temos que

para
![x\in [-2,\, 1] x\in [-2,\, 1]](/latexrender/pictures/827a169ef687cf6140e6899db2883074.png)
.
Isso significa que para determinar a área entre a reta e a parábola nesse intervalo, vamos precisar calcular a integral:
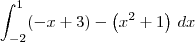
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucat28 » Dom Set 04, 2011 11:45
por lucat28 » Dom Set 04, 2011 11:45
Perfeito Luiz, agora sim entendi.
muito obrigado

-
lucat28
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 16, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- AREA LIMITADA
 por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
- 3 Respostas
- 7167 Exibições
- Última mensagem por admin

Ter Ago 26, 2008 19:02
Cálculo: Limites, Derivadas e Integrais
-
- Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58
- 1 Respostas
- 1944 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02
- 0 Respostas
- 1133 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:04
- 1 Respostas
- 1516 Exibições
- Última mensagem por matmatco

Sáb Ago 09, 2014 12:15
Cálculo: Limites, Derivadas e Integrais
-
- Área de Região plana limitada por funções
 por iarapassos » Qui Jan 03, 2013 18:52
por iarapassos » Qui Jan 03, 2013 18:52
- 1 Respostas
- 2675 Exibições
- Última mensagem por Russman

Qui Jan 03, 2013 20:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
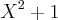 e pela reta y =
e pela reta y = 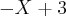




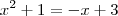
 para
para ![x\in [-2,\, 1] x\in [-2,\, 1]](/latexrender/pictures/827a169ef687cf6140e6899db2883074.png) .
.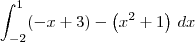

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.