 por henriquefreitas » Seg Ago 22, 2011 20:24
por henriquefreitas » Seg Ago 22, 2011 20:24
Num concurso passaram 12% dos candidatos que fizeram as provas dos 17.500 candidatos inscritos 8% faltaram as provas Qual o numero de candidatos aprovados.
Por Favor me ajuda ae
-
henriquefreitas
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Ago 22, 2011 21:23
por Molina » Seg Ago 22, 2011 21:23
Boa noite, Henrique.
Calcule primeiramente isso...
henriquefreitas escreveu:dos 17.500 candidatos inscritos 8% faltaram as provas
Ou seja, 8% de 17500.
O resultado subtraia de 17500, pois assim ficará quem participou da prova.
Posteriormente, calcule...
henriquefreitas escreveu:12% dos candidatos que fizeram as provas
Ou seja, 12% deste número que você calculou primeiro.
Qualquer dúvida, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por henriquefreitas » Seg Ago 22, 2011 21:29
por henriquefreitas » Seg Ago 22, 2011 21:29
aee brother so nao entendi a parte dos 12 % resolvi certinho a primeira mais dos 12 ali me perdi pode me ajuda ?
-
henriquefreitas
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Ago 22, 2011 21:38
por Molina » Seg Ago 22, 2011 21:38
henriquefreitas escreveu:aee brother so nao entendi a parte dos 12 % resolvi certinho a primeira mais dos 12 ali me perdi pode me ajuda ?
Certo. Vamos fazer juntos.
A primeira parte você fez, certo? Então dos 17500 inscritos, tirando os 8% que faltaram, quantos realizaram o concurso?
Vou chamar este valor que você encontrou de
XOu seja, na segunda parte o que você quer saber é
quanto vale 12% deste número X.
Coloque suas tentativas para que eu possa continuar te ajudando.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por henriquefreitas » Seg Ago 22, 2011 21:48
por henriquefreitas » Seg Ago 22, 2011 21:48
ta fiz 8% de 17500 deu 1400 e os 12 que eu to me perdendo =/
-
henriquefreitas
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Ago 22, 2011 21:58
por Molina » Seg Ago 22, 2011 21:58
OK.
Esse 1400 foram os que não fizeram prova. Com isso temos absoluta certeza que:
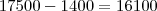
fizeram a prova.
Tudo certo até aqui?
Agora calcule 12% de 16100.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por henriquefreitas » Seg Ago 22, 2011 22:07
por henriquefreitas » Seg Ago 22, 2011 22:07
agora sim brother entendi agora valeu por me ajuda super abraçao.

-
henriquefreitas
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4582 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7912 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3750 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3682 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2919 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









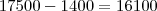 fizeram a prova.
fizeram a prova.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.