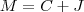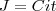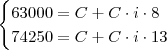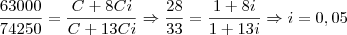por Tito » Dom Ago 21, 2011 05:30
por Tito » Dom Ago 21, 2011 05:30
Olá pessoal...
Este problema me parece bem simples mas não consigo resolve-lo. Tentei da seguinte forma conforme o enunciado.
(BB) Se aplicarmos determinada quantia durante 8 meses, seu montante será de $ 63.000. Caso a aplicação durasse 13 meses, o montante seria de $ 74.250. Qual a taxa mensal empregada...
Eu fiz os seguintes cálculos colocando o montante de 63.000 como capital.
C: 63.000
M: 74.250
J: 74.250 - 63.000 = 11.250
T: 13 - 8 = 5 meses
J=P%C
11.250=P%63.000
P%=0,1786 = 17,86%
P%=i x t
17,86=i x 5
i=3,572
A resposta correta é 5%.
Obrigado.
-
Tito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 21, 2011 05:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmacêutico
- Andamento: formado
 por Caradoc » Dom Ago 21, 2011 11:16
por Caradoc » Dom Ago 21, 2011 11:16
Você pode fazer um sistema:
O montante é o capital + juros
E os juros são o capital * taxa * tempo
Então:
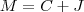
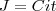
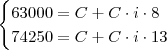
Com duas equações e duas incógnitas você consegue resolver o sistema.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Tito » Ter Ago 23, 2011 01:52
por Tito » Ter Ago 23, 2011 01:52
Obrigado Caradoc, demorei mas consegui resolver pelo seu sistema..
Eu peguei a primeira sentença e negativei: -63.000 = -C -Ci8
depois fiz adição de sistemas com: 74.250 = C + Ci13
isolei o "C": C = 2250/i
e substitui na primeira sentença do sistema.
encontrei 0,05 = 5%
-
Tito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 21, 2011 05:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmacêutico
- Andamento: formado
 por LuizAquino » Ter Ago 23, 2011 09:47
por LuizAquino » Ter Ago 23, 2011 09:47
Tito escreveu:Eu peguei a primeira sentença e negativei: -63.000 = -C -Ci8
depois fiz adição de sistemas com: 74.250 = C + Ci13
isolei o "C": C = 2250/i
e substitui na primeira sentença do sistema.
encontrei 0,05 = 5%
Nesse caso bastava dividir membro a membro a primeira equação pela segunda. Isto é, resolver a equação:
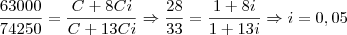
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em montante e taxa de juros.
por Marcosaf » Seg Set 15, 2014 14:41
- 3 Respostas
- 3983 Exibições
- Última mensagem por jcmatematica

Ter Set 16, 2014 16:50
Matemática Financeira
-
- [Montante captalizado] Encontrar montante captalizado
por donizeth » Sex Jun 07, 2013 09:03
- 0 Respostas
- 1402 Exibições
- Última mensagem por donizeth

Sex Jun 07, 2013 09:03
Matemática Financeira
-
- Juro Composto - Encontrar taxa
por zero_br » Qui Dez 06, 2012 18:04
- 0 Respostas
- 2043 Exibições
- Última mensagem por zero_br

Qui Dez 06, 2012 18:04
Matemática Financeira
-
- Juros, Encontrar Taxa Mensal
por elisamaria » Seg Mar 09, 2015 16:20
- 0 Respostas
- 2413 Exibições
- Última mensagem por elisamaria

Seg Mar 09, 2015 16:20
Matemática Financeira
-
- Encontrar a taxa efetiva anual da operação
 por cristianetimmbonow » Seg Mar 20, 2017 10:54
por cristianetimmbonow » Seg Mar 20, 2017 10:54
- 0 Respostas
- 4684 Exibições
- Última mensagem por cristianetimmbonow

Seg Mar 20, 2017 10:54
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.