 por sempre_aprendendo » Qui Ago 18, 2011 11:14
por sempre_aprendendo » Qui Ago 18, 2011 11:14
Um determinado capital aplicado a juros simples exatos a uma certa taxa anual rendeu R$240. Determine os juros auferidos nessa aplicação se fossem comerciais.
Fiz um cálculo e descobri o valor, porém não sei explicar ao professor a resolução.
Juro Anual Exato = 365 dias/ano
Juro Anual Comercial = 360 dias/ano
240*365= 87600
87600/360= 243,33
O resultado está correto, porém não sei como explicar a forma correta da solução. Qual outra forma de chegar nesse resultado?
Escrevendo o que li fica mais ou menos assim:
C+i/365*1=240 = J¹
C+i/360*1= J²
ou
240/365 = 0.6575 seria isso os juros diários?
-
sempre_aprendendo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Ago 18, 2011 10:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Caradoc » Sex Ago 19, 2011 13:47
por Caradoc » Sex Ago 19, 2011 13:47
Vamos considerar que o dinheiro ficou aplicado por t dias à uma taxa anual constante.
A diferença entre os dois tipos de juros é que se considerarmos o ano com 360 dias, a taxa diária, que é a taxa anual dividida pelo número de dias no ano será maior do que se considerarmos o ano com 365 dias.
Então temos que a taxa diária simples e a taxa diária comercial são:
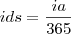
e
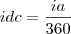
Então temos que:
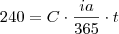
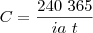
Agora mudando a taxa diária para a comercial e substituindo o valor do capital:
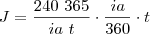
Simplificando chegamos que:
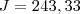
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desconto comercial simples
por Larice Mourao » Qua Nov 21, 2012 21:19
- 2 Respostas
- 5315 Exibições
- Última mensagem por Larice Mourao

Qui Nov 22, 2012 13:32
Matemática Financeira
-
- Problema envolvendo desconto comercial simples
por Ju_Petrokis » Qua Set 16, 2009 20:00
- 1 Respostas
- 2575 Exibições
- Última mensagem por Victor Emanuel

Qui Set 24, 2009 15:30
Matemática Financeira
-
- [Juros Composto] Desconto comercial composto
por DPassos » Qui Mar 05, 2015 18:18
- 2 Respostas
- 5721 Exibições
- Última mensagem por Russman

Sex Mar 06, 2015 00:37
Matemática Financeira
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8219 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- Juros Simples
por Gir » Ter Set 01, 2009 11:03
- 1 Respostas
- 8309 Exibições
- Última mensagem por Lucio Carvalho

Ter Set 01, 2009 17:24
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


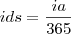
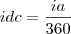
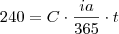
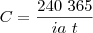
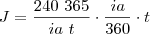
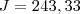

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.