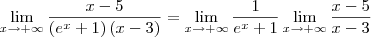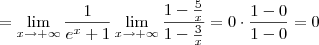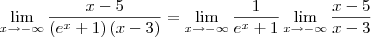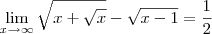Só consegui fazer assim:
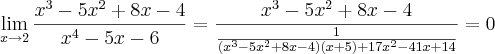
não sei se a ideia da manipulaçao algébrica esta correta... no caso fazer a divisao do denominador pelo numerador atraves do método da chave encontrando uma resposta e colocando ela como denominador e no numerador 1. ou seja, seria a resposta da primeira divisao elevada a -1 ja que o expoente do denominador é de 1 grau menor que o do numerador.
nao tenho gabarito para corrigir.
Outra questao que nao consigo é:
![\lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1} \lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1}](/latexrender/pictures/190833bac7797bdc3143e90e07c91104.png)
O estranho é que o professor não nos ensinou aquele método que vocês costumam usar aqui no fórum que é de substituir determinado termo por uma outra letra etc. Não sei nem dizer se isso é pra ser estudado agora ou só mais tarde. Alguém me ajuda?


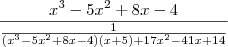
![= (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right] = (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right]](/latexrender/pictures/e942348fc8df8f63916cb606c2e4cf3f.png)

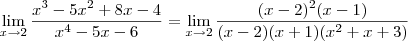
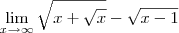
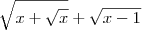 :
: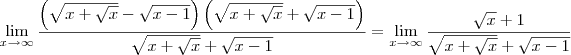
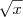 :
: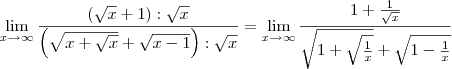

![\frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}} \frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}}](/latexrender/pictures/f499b7d38ffc7736042e9571b020b535.png)
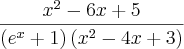
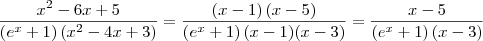
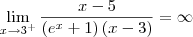
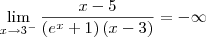
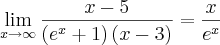 (dividi todos os termos por x
(dividi todos os termos por x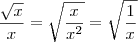
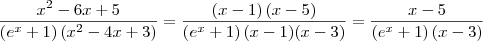
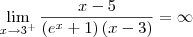
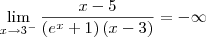
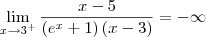
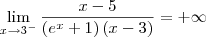
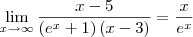 (dividi todos os termos por x
(dividi todos os termos por x