 por -civil- » Qua Ago 10, 2011 16:16
por -civil- » Qua Ago 10, 2011 16:16
Boulos - 3ª ed. - Cap. 18
18-9) O segmento BE é a base de um triângulo isósceles de vértice A e é também a intersecção desse triângulo com o retângulo de vértices B, C, D, E. Os cinco pontos são coplanares. Conhecendo A = (1,1,0), B = (2,0,1) e C = (6,-2,3), obtenha as coordenadas de D e E (SO).Como o triângulo ABE é isóceles, cada ângulo interno tem 60º.
Considerando E = (
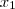
,
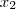
,
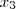
)
||
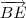
||.||
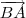
||. cos 60º =
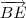
.
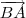
3.

= ( - 2,
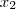
,
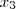
- 1).(-1,1,-1)
1)
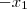
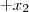
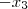
+

= 0
dist(B,A) =

=

= dist (B,E)
dist(B,E) =

=

2) (
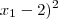
+ (
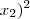
+ (
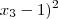
= 3
Como consigo encontrar mais equações para achar essas incógnitas do ponto E?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Ago 11, 2011 23:50
por LuizAquino » Qui Ago 11, 2011 23:50
-civil- escreveu:Como o triângulo ABE é isóceles, cada ângulo interno tem 60º.
Já começa errado daqui! Um triângulo
isósceles não necessariamente tem todos os ângulos internos iguais a 60°.
O que temos a priori sobre um triângulo isósceles é que os ângulos da base são congruentes. Além disso, os seus dois lados que não são a base também são congruentes.
A figura abaixo ilustra o exercício.
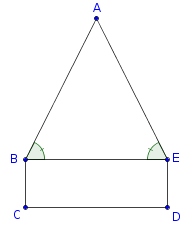
- triângulo_isósceles_e_retângulo.png (4.09 KiB) Exibido 2431 vezes
Já que ABE é isósceles e A, B, C e E são coplanares, para determinar o ponto E você pode usar três informações:
- ele está no mesmo plano que contém A, B e C;
-
 ;
; - Os ângulos
 e
e 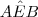 são congruentes.
são congruentes.
Por outro lado, como BCDE é um retângulo, para determinar D basta usar o fato de que
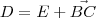
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por -civil- » Qui Ago 18, 2011 00:11
por -civil- » Qui Ago 18, 2011 00:11
Seguindo as suas dicas tenho que :

é o plano formado por A, B e C

= (1,-1,1) e
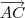
= (5,-3,3)

: X = (1,1,0) +

(1,-1.1) +

(5,-3,3)
E = (

,
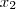
,
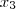
)
||
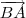
|| = ||
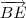
||

=

3 =
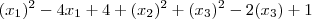
Usando que

e
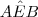
:
||

||.||
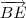
||.cos

= ||
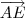
||.||
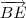
||.cos

||

|| = ||
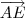
||
Desculpe mas fiquei na mesma, ainda não sei como encontrar o ponto E
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Ago 18, 2011 10:15
por LuizAquino » Qui Ago 18, 2011 10:15
-civil- escreveu:Seguindo as suas dicas tenho que :

é o plano formado por A, B e C

= (1,-1,1) e
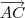
= (5,-3,3)

: X = (1,1,0) +

(1,-1.1) +

(5,-3,3)
Ok. Mas, agora encontre a equação geral (cartesiana) do plano. Vamos chamar essa equação de (1).
-civil- escreveu:E = (

,
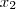
,
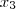
)
||
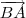
|| = ||
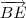
||

=

3 =
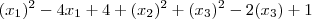
Isso está errado. Note que você deve fazer

. Refaça as suas contas considerando essa informação. Vamos chamar essa equação de (2).
-civil- escreveu:Usando que

e
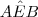
:
||

||.||
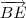
||.cos

= ||
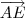
||.||
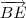
||.cos

||

|| = ||
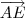
||
Isso também está errado.
Para o ângulo

temos que:
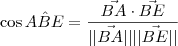
.
Já para o ângulo
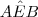
temos que:
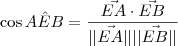
.
Como esses ângulos são iguais, temos que
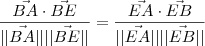
. Como

e

, no final ficamos com

. Vamos chamar essa equação de (3).
Agora, com as equações (1), (2) e (3) você monta um sistema (não linear) com 3 equações e 3 incógnitas. Basta resolvê-lo e você determina o ponto E.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Encontrar a reta t
por -civil- » Ter Ago 09, 2011 21:49
- 1 Respostas
- 2213 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 23:31
Geometria Analítica
-
- Encontrar equação (vetorial) da reta
por elisafrombrazil » Qua Abr 19, 2017 21:52
- 0 Respostas
- 1820 Exibições
- Última mensagem por elisafrombrazil

Qua Abr 19, 2017 21:52
Álgebra Linear
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2418 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [Geometria Analítica] - Encontrar o módulo de s.
por Nicolas1Lane » Dom Mar 23, 2014 00:33
- 2 Respostas
- 1694 Exibições
- Última mensagem por Nicolas1Lane

Dom Mar 23, 2014 19:13
Geometria Analítica
-
- [Geometria Analítica] Encontrar os vértices do hexágono
 por -civil- » Qua Ago 10, 2011 16:51
por -civil- » Qua Ago 10, 2011 16:51
- 1 Respostas
- 2089 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 12:44
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
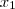 ,
, 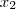 ,
, 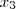 )
)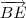 ||.||
||.||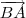 ||. cos 60º =
||. cos 60º = 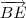 .
.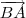
 = ( - 2,
= ( - 2, 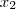 ,
, 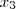 - 1).(-1,1,-1)
- 1).(-1,1,-1)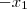
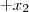
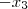 +
+  = 0
= 0 =
=  = dist (B,E)
= dist (B,E) =
= 
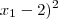 + (
+ (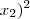 + (
+ (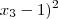 = 3
= 3

 ;
; e
e 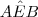 são congruentes.
são congruentes.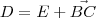 .
.
 é o plano formado por A, B e C
é o plano formado por A, B e C = (1,-1,1) e
= (1,-1,1) e 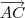 = (5,-3,3)
= (5,-3,3) (1,-1.1) +
(1,-1.1) +  (5,-3,3)
(5,-3,3) ,
,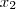 ,
,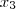 )
)
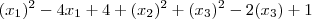
 = ||
= ||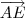 ||.||
||.||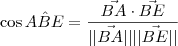 .
. .
. . Como
. Como  , no final ficamos com
, no final ficamos com  . Vamos chamar essa equação de (3).
. Vamos chamar essa equação de (3).




