Calcule o volume do tetraedro (SO) determinado pelas retas r, s, t e pelo plano
 , nos casos:
, nos casos:(a)
 : x + y + z - 5 = 0
: x + y + z - 5 = 0r: x = z = 0
s:x = y = 0
t: x - 2y = z = 0
Primeiramente passei as equações da reta para a forma vetorial. Ficou:
r: X = (0,0,0) +
 (0,1,0)
(0,1,0)s: X = (0,0,0) +
 (0,0,1)
(0,0,1)t: X = (0,0,0) +
 (2,1,0)
(2,1,0)Daí eu igualei cada uma com a equação do plano

r: X = (0,0,0) +
 (0,1,0)
(0,1,0) : 0 +
: 0 +  + 0 - 5 = 0
+ 0 - 5 = 0 = 5
= 5A= (0,5,0)
s: X = (0,0,0) +
 (0,0,1)
(0,0,1) : 0 + 0 +
: 0 + 0 + - 5 = 0
- 5 = 0 = 5
= 5B = (0,0,5)
t: X = (0,0,0) +
 (2,1,0)
(2,1,0) : 2
: 2 +
+  + 0 - 5 = 0
+ 0 - 5 = 03
 = 5
= 5 = 5/3
= 5/3C = (0,5/3,0)
Eu entendi que o ponto de intersecção de r, s e t é O = (0,0,0)
Então o volume do tetraedro seria:
![\frac{1}{6} [\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}] \frac{1}{6} [\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}]](/latexrender/pictures/089120171cf9e3a4f29a47b7756e60ca.png)
Só que o resultado é zero! O que eu estou fazendo de errado?


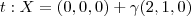

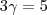
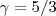

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)