 por LuizCarlos » Dom Ago 07, 2011 19:44
por LuizCarlos » Dom Ago 07, 2011 19:44
Ola, não estou conseguindo resolver esse exercício.
A sentença
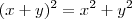
não é uma identidade.
A) Descubra valores de x e de y para os quais
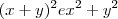
apresentem resultados diferentes e outros para os quais apresentem resultados iguais.
Ja tentei varios tipos de valores pra x e y, mas não da igual o resultado.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Dom Ago 07, 2011 20:09
por Molina » Dom Ago 07, 2011 20:09
Boa noite.
Perceba que

Então o que você quer encontrar são os valores que:

Consegue seguir daqui?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Dom Ago 07, 2011 20:46
por LuizCarlos » Dom Ago 07, 2011 20:46
Molina escreveu:Boa noite.
Perceba que

Então o que você quer encontrar são os valores que:

Consegue seguir daqui?
OK, Diego, essa parte eu entendi, mas tipo, eu vou colocando valores para x e y, observe.
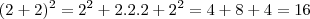
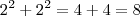
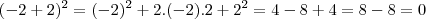
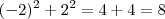
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Dom Ago 07, 2011 20:50
por Molina » Dom Ago 07, 2011 20:50
Boa noite.
Você não vai resolver esta questão testando valores. É necessário um modo mais simples de encontrar os valores para o que queremos.
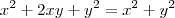
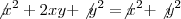
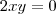
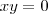
Ou seja, ou

ou

. Essas é a condição para que isso ocorra.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Dom Ago 07, 2011 20:59
por LuizCarlos » Dom Ago 07, 2011 20:59
Molina escreveu:Boa noite.
Você não vai resolver esta questão testando valores. É necessário um modo mais simples de encontrar os valores para o que queremos.
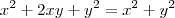
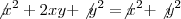
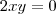

Ou seja, ou

ou

. Essas é a condição para que isso ocorra.

Ok, entendi a questao de ou o x é sero ou o y é zero, mas agora você cancelou o
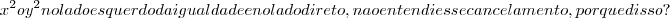
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Dom Ago 07, 2011 21:01
por LuizCarlos » Dom Ago 07, 2011 21:01
LuizCarlos escreveu:Molina escreveu:Boa noite.
Você não vai resolver esta questão testando valores. É necessário um modo mais simples de encontrar os valores para o que queremos.
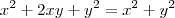
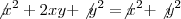
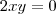

Ou seja, ou

ou

. Essas é a condição para que isso ocorra.

Ok, entendi a questao de ou o x é zero ou o y é zero, mas agora você cancelou o
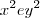
no lado esquerdo da igualdade e no lado direto, nao entendi esse cancelamento, por que disso ?
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Seg Ago 08, 2011 01:51
por MarceloFantini » Seg Ago 08, 2011 01:51
Porque são termos dos dois lados. É como se fosse

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8654 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3121 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8720 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2458 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 3951 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
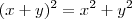 não é uma identidade.
não é uma identidade.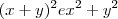 apresentem resultados diferentes e outros para os quais apresentem resultados iguais.
apresentem resultados diferentes e outros para os quais apresentem resultados iguais.
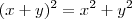 não é uma identidade.
não é uma identidade.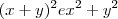 apresentem resultados diferentes e outros para os quais apresentem resultados iguais.
apresentem resultados diferentes e outros para os quais apresentem resultados iguais.



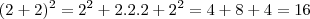
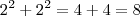
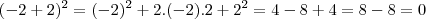
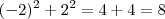

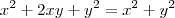
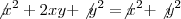
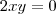

 ou
ou  . Essas é a condição para que isso ocorra.
. Essas é a condição para que isso ocorra.

ou
. Essas é a condição para que isso ocorra.
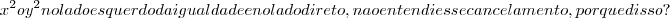

ou
. Essas é a condição para que isso ocorra.
no lado esquerdo da igualdade e no lado direto, nao entendi esse cancelamento, por que disso ?



 .
.



