É dado essa informação:
se cos x = 1/3 então sen x = 2(raiz)2/3

Como foi descoberto esse valor sen 2(raiz)2/3 somente com a ajuda do cos 1/3 e o lado 1?????
Tentei diferentes formas, mas somente achei o resultado 2/3 para o seno.





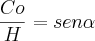
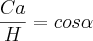
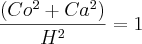
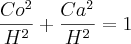
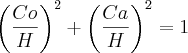
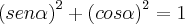
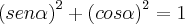
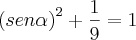
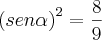
![sen\alpha=\sqrt[]{\frac{8}{9}} sen\alpha=\sqrt[]{\frac{8}{9}}](/latexrender/pictures/29e648d2a88bbd9d48a28ea260057228.png)
![sen\alpha=\frac{\sqrt[]{8}}{3} sen\alpha=\frac{\sqrt[]{8}}{3}](/latexrender/pictures/62adc1513e3545e2b01da80def0ceb6d.png)
![sen\alpha=\frac{2.\sqrt[]{2}}{3} sen\alpha=\frac{2.\sqrt[]{2}}{3}](/latexrender/pictures/f17c7cbac7684f798c52708119aa6b11.png)


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)