Oí amigos! Tudo bem?
Estou estudando para um concurso e resolvendo algumas questões, porém fiquei com dúvidas nas seguintes questões abaixo:
a) lim t³+4t²+4t OBS: Numerador e Denominador, foi pq não tive como colocar a
t=>-2 (t+2)(t-3) a barra da divisão.
b) lim f(x)
x tendendo ao infinito
c) lim (1+1/n)n+5 OBS: o termo n+5 é o expoente.
x tendendo ao infinito
d) f(x) = x-(x) em x=0 OBS: Os parenteses são módulos.
Se alguém ficar na dúvida sobre algo, pode me mandar um e-mail, que passo as questões:
fabiodultra@gmail.com
Desde já agradeço a atenção de todos.
Abraços...
Até mais.



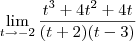
 do denominador.
do denominador. em evidência:
em evidência: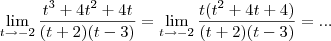


 com
com 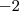 ),
), 

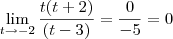
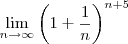
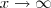 e eu acreditei ser
e eu acreditei ser 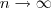 )
)![\lim_{n\rightarrow \infty} \left( 1 + \frac1n \right)^{n+5}
=
\lim_{n\rightarrow \infty}
\left[
\left( 1 + \frac1n \right)^n
\left( 1 + \frac1n \right)^5
\right] = \cdots \lim_{n\rightarrow \infty} \left( 1 + \frac1n \right)^{n+5}
=
\lim_{n\rightarrow \infty}
\left[
\left( 1 + \frac1n \right)^n
\left( 1 + \frac1n \right)^5
\right] = \cdots](/latexrender/pictures/2d4402d32ba5f56bf6ded10244503477.png)
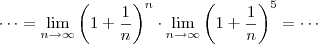
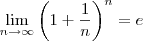
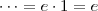
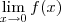 , onde
, onde 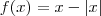

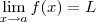 se e somente se
se e somente se 
 para
para 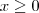 , temos:
, temos: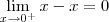
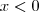 , temos
, temos 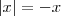 , assim:
, assim: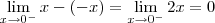
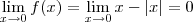
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.