Página 85
Exercício 3
Dada a função
 , verifique que
, verifique que  . Pergunta-se: f é contínua em 1? Por Quê?
. Pergunta-se: f é contínua em 1? Por Quê?De acordo com meus cálculos encontrei

Ou seja, se os limites laterais pela esquerda e pela direita são iguais, determinei, que a função é contínua.
O que no gabarito esta dizendo o contrário.










 e
e 

 .
.
 .
.
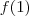
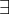



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)