Ando a estudar para Teoria dos Anéis e surgiu-me uma dúvida de uma demonstração:
Teorema: se R é Anel comutativo com 1 no qual valem as Leis do Cancelamento, então R é Domínio de Integridade.
DEM:
Sendo R um Domínio de Integridade;
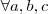
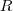
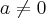;Tal que:
então:
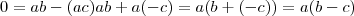e como a é diferente de 0 => 
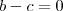, ou seja, 
O que eu não entendo é o facto de dizerem:
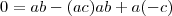
Se alguém me puder explicar o porquê desta igualdade, ficarei muito agradecido, penso que seja pela unicidade do oposto, mas não entendo a lógica disto!! :|
m0x0
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)