 por aline_n » Qui Jul 14, 2011 16:24
por aline_n » Qui Jul 14, 2011 16:24
Duas empresas foram contratadas para realizar um estudo ambientalem um certo municipio. A empresa A relevou que a concentracao media de moxido de carbono em funcao do tempo t é dado pela lei de formacao
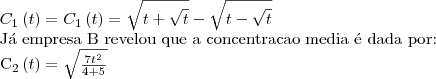
[/tex]
A longo prazo quai das concentracoes medias de monoxido de carbono sera maior
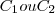
Tentei responder assim:
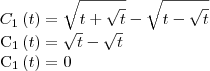
??????
-
aline_n
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 28, 2011 09:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por Molina » Qui Jul 14, 2011 16:34
por Molina » Qui Jul 14, 2011 16:34
Boa tarde.
Esta passagem aqui não está correta:
aline_n escreveu: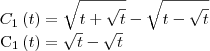
Você está considerando que
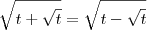
e isso não é verdade.
Veja que, por exemplo,
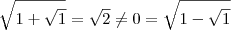
Perceba que o assunto é aplicação de limite. Ou seja, em ambas a função faça o limites dela tendendo ao infinito
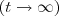
Qualquer dúvida informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por aline_n » Qui Jul 14, 2011 16:51
por aline_n » Qui Jul 14, 2011 16:51
Posso multiplicar ambas as funçoes pelo seus conjugados ????
-
aline_n
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 28, 2011 09:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por Molina » Qui Jul 14, 2011 16:59
por Molina » Qui Jul 14, 2011 16:59
Confirmando as funções:

e
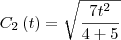
Por que na segunda, a parte do denominados já não está somada?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- aplicaçao de EDO
por nayana_ac » Dom Set 19, 2010 01:28
- 3 Respostas
- 15284 Exibições
- Última mensagem por Krilitolxc

Ter Fev 02, 2016 07:40
Problemas do Cotidiano
-
- prazo de aplicação?
por aprendiz da vida » Seg Mai 10, 2010 16:29
- 2 Respostas
- 8203 Exibições
- Última mensagem por aprendiz da vida

Seg Mai 10, 2010 18:02
Matemática Financeira
-
- Aplicação Linear
por TiagoFERD » Sex Dez 30, 2011 17:42
- 2 Respostas
- 8049 Exibições
- Última mensagem por TiagoFERD

Sex Dez 30, 2011 20:15
Álgebra Elementar
-
- [Aplicação Financeira]
por gustavowelp » Sex Nov 02, 2012 10:05
- 1 Respostas
- 7499 Exibições
- Última mensagem por young_jedi

Sex Nov 02, 2012 12:42
Matemática Financeira
-
- Integral com aplicaçao
 por menino de ouro » Dom Jan 13, 2013 17:11
por menino de ouro » Dom Jan 13, 2013 17:11
- 5 Respostas
- 9396 Exibições
- Última mensagem por Russman

Dom Jan 13, 2013 22:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
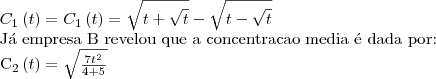 [/tex]
[/tex]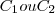
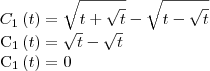

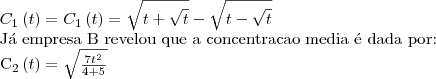 [/tex]
[/tex]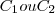
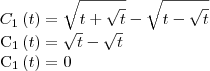

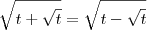 e isso não é verdade.
e isso não é verdade.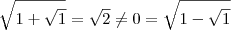
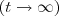




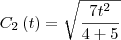



 , avisa que eu resolvo.
, avisa que eu resolvo.

