





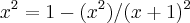 ...q. sera o polinomio:
...q. sera o polinomio: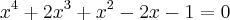 ...tomamos p(x)=
...tomamos p(x)=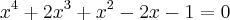
![{y}=\sqrt[2]{1-{x}^{2}} {y}=\sqrt[2]{1-{x}^{2}}](/latexrender/pictures/e0237593d02a61b2449918ff548936d5.png) ...
...![\sqrt[2]{1-{x}^{2}} \sqrt[2]{1-{x}^{2}}](/latexrender/pictures/84e0b92deaa020377a0d256463bbab3d.png) ...dA/dx=0
...dA/dx=0 x=1/2...vamos estudar o intervalo[0,1/2],temos q.
x=1/2...vamos estudar o intervalo[0,1/2],temos q.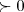
 um num.par de raizes em[0,1/2]ou nenhuma raiz...sejam
um num.par de raizes em[0,1/2]ou nenhuma raiz...sejam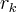 as raizes p/k=1,...,4,entao tomando o produto de (0-
as raizes p/k=1,...,4,entao tomando o produto de (0-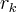 ).(1/2-
).(1/2-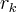 )
)
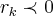 ,o q. contradiz,pois os num.em [0,1/2]sao todos positivos,logo nao existem raizes em [0,1/2],tal q. p(x)=0...como x=1/2 e o max.valor q. x pode tomar,entao x=1/2 e a resposta...
,o q. contradiz,pois os num.em [0,1/2]sao todos positivos,logo nao existem raizes em [0,1/2],tal q. p(x)=0...como x=1/2 e o max.valor q. x pode tomar,entao x=1/2 e a resposta...
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

