 por joaofonseca » Dom Jul 03, 2011 11:54
por joaofonseca » Dom Jul 03, 2011 11:54
Nas funções racionais existe um caso especial, em que substituindo a variável independente por um valor, se obtem zero tanto no numerador como no denominador.
Exemplo:
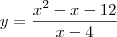
Li algures que o contradominio de uma função são todos os valores de
y possíveis quando se substituí a variável independente por todos os valores possíveis para o dominio.
Analisando a função, posso concluír que não existem assintotas horizontais, e que a possível assintota vertical também não existe pois 4 anula tanto o denominador como o numerador. É precisamente em
x=4 que existe um buraco no gráfico da função, diz-se que a função não está definida nesse ponto.
Simplificando:
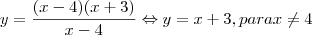
Posso concluír que o

?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Renato_RJ » Dom Jul 03, 2011 12:51
por Renato_RJ » Dom Jul 03, 2011 12:51
Bom dia João...
Seguinte, você já viu que o polinômio do numerador é divisível pelo do denominador, logo a sua função racional é
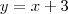
, logo
o domínio (conjunto onde encontramos os valores para a variável x) será

enquanto que o seu contradomínio (conjunto com os valores de y) será

. Não entendi porque o seu contradomínio é
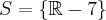
, ou você queria dizer que o seu domínio é esse ?? Pois em x=7 não existe indeterminação da função.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por joaofonseca » Dom Jul 03, 2011 13:29
por joaofonseca » Dom Jul 03, 2011 13:29
Renato_RJ abrigado,
Bem sei que a função
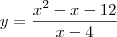
não está na forma irredutível. Por isso tem um fator comum, que é x-4. Por outro lado y=x+3 é a assintota obliqua.
Na expressão original, sabemos que x tem de ser diferente de 4 pois anularia o denominador, logo 4 não faz parte do dominio da função. Por isso quando se simplifica a expressão para y=x+3 é para valores diferentes de 4.
Como 4 anula também o numerador, x=4 não é uma assintota vertical.
Substituindo x por 4 em y=x+3 obten-se y=7, por isso concluí que se a função não está definida para (4,y), o y é igual a 7.
Se o dominio são todos os números reais exeto o 4 o contradominio serão todos os números reais exeto o 7.
Está é a minha dúvida.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jul 03, 2011 13:36
por MarceloFantini » Dom Jul 03, 2011 13:36
O contradomínio de uma função é o conjunto onde ela
pode assumir valores, mas que não necessariamente o faz. Exemplo:
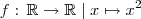
. Note que a função nunca retornará um valor negativo, entretanto a priori ela pode. Então o contradomínio pode ser os reais, mas a imagem será
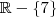
na sua questão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Renato_RJ » Dom Jul 03, 2011 14:09
por Renato_RJ » Dom Jul 03, 2011 14:09
Agora eu entendi a sua dúvida João, mas o Fantini já respondeu...
Grato Fantini....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por telmojc » Qui Fev 09, 2012 15:22
por telmojc » Qui Fev 09, 2012 15:22
nao sei se o seu pensamento está correcto mas uma maneira facil de saber o contradominio é calcular funçao inversa, e ver o dominio desta que será o contradominio da função normal
-
telmojc
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Fev 09, 2012 15:13
- Formação Escolar: EJA
- Andamento: cursando
 por LuizAquino » Qui Fev 09, 2012 16:57
por LuizAquino » Qui Fev 09, 2012 16:57
telmojc escreveu:nao sei se o seu pensamento está correcto mas uma maneira facil de saber o contradominio é calcular funçao inversa, e ver o dominio desta que será o contradominio da função normal
Por favor, leia o tópico:
Funções e Limitesviewtopic.php?f=107&t=7094
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por telmojc » Qui Fev 09, 2012 19:04
por telmojc » Qui Fev 09, 2012 19:04
ah ok
ainda não aprendi a calcular o contra dominio por limites mas acho que aprendo ainda este mês
-
telmojc
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Fev 09, 2012 15:13
- Formação Escolar: EJA
- Andamento: cursando
 por MarceloFantini » Qui Fev 09, 2012 19:07
por MarceloFantini » Qui Fev 09, 2012 19:07
O contradomínio é dado, e não calculado. A única pergunta relacionado a isso que pode fazer sentido é "encontre o maior contradomínio possível", pois podem existir vários.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Fev 10, 2012 10:52
por LuizAquino » Sex Fev 10, 2012 10:52
MarceloFantini escreveu:O contradomínio é dado, e não calculado. A única pergunta relacionado a isso que pode fazer sentido é "encontre o maior contradomínio possível", pois podem existir vários.
Outra questão que também faz sentido seria: "encontre o
menor contradomínio possível".
Entretanto, essa questão poderia ser reescrita como: "encontre a imagem".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Contradomínio de uma função(exercício)
por rebeca10 » Qua Jul 31, 2013 21:34
- 1 Respostas
- 2350 Exibições
- Última mensagem por e8group

Qua Jul 31, 2013 21:46
Funções
-
- [Contradomínio de um função exponencial]
por senhoradragneel96 » Sáb Jan 11, 2014 15:05
- 0 Respostas
- 4393 Exibições
- Última mensagem por senhoradragneel96

Sáb Jan 11, 2014 15:05
Funções
-
- Integral de função racional
por renan_a » Qua Jan 09, 2013 17:57
- 2 Respostas
- 1982 Exibições
- Última mensagem por renan_a

Qua Jan 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Limite de Função Racional
por joaofonseca » Qua Mai 04, 2011 20:50
- 3 Respostas
- 2365 Exibições
- Última mensagem por LuizAquino

Qua Mai 04, 2011 23:53
Cálculo: Limites, Derivadas e Integrais
-
- Função Racional! Ajuda urgente
por renatofbc » Qua Jun 22, 2011 22:33
- 2 Respostas
- 2239 Exibições
- Última mensagem por MarceloFantini

Qua Jun 22, 2011 23:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
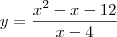
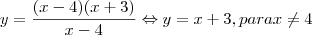
 ?
?

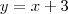 , logo
, logo  enquanto que o seu contradomínio (conjunto com os valores de y) será
enquanto que o seu contradomínio (conjunto com os valores de y) será 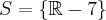 , ou você queria dizer que o seu domínio é esse ?? Pois em x=7 não existe indeterminação da função.
, ou você queria dizer que o seu domínio é esse ?? Pois em x=7 não existe indeterminação da função.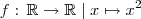 . Note que a função nunca retornará um valor negativo, entretanto a priori ela pode. Então o contradomínio pode ser os reais, mas a imagem será
. Note que a função nunca retornará um valor negativo, entretanto a priori ela pode. Então o contradomínio pode ser os reais, mas a imagem será 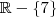 na sua questão.
na sua questão.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
