 por Maykids » Qua Jun 29, 2011 12:33
por Maykids » Qua Jun 29, 2011 12:33
Para quais valores de m a reta y=mx e a curva
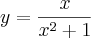
limitam uma região? Encontre a área da região.
eu comecei igualando as duas,
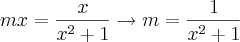
mais daqui pra frente empaquei, alguma dica ai pessoal? eu ja tentei simular de como seria as curvas, mais nada =/
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Qua Jun 29, 2011 16:22
por LuizAquino » Qua Jun 29, 2011 16:22
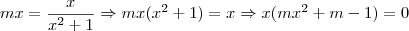
Disso, segue que

e
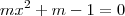
.
Agora, lembre-se que uma equação polinomial do 2º grau dada por
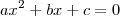
tem solução real quando
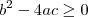
. Atenção! Cuidado ao identificar os coeficientes a, b e c da equação
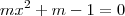
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites descobrindo Valores
por Maykids » Sáb Jul 09, 2011 01:19
- 1 Respostas
- 1073 Exibições
- Última mensagem por LuizAquino

Ter Jul 12, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- [Integral tripla]definir valores para cálculo
 por jeferson_justo135 » Qua Jan 14, 2015 21:24
por jeferson_justo135 » Qua Jan 14, 2015 21:24
- 5 Respostas
- 3470 Exibições
- Última mensagem por jeferson_justo135

Dom Fev 08, 2015 15:51
Cálculo: Limites, Derivadas e Integrais
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5161 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- Descobrindo os casais
por Cleyson007 » Dom Fev 07, 2010 14:18
- 1 Respostas
- 1485 Exibições
- Última mensagem por Elcioschin

Seg Fev 08, 2010 22:37
Desafios Médios
-
- DESCOBRINDO OS DIVISORES DA TAXA i%
por leo_30_rj » Sáb Ago 14, 2010 17:17
- 2 Respostas
- 1755 Exibições
- Última mensagem por Douglasm

Seg Ago 16, 2010 13:59
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
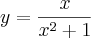 limitam uma região? Encontre a área da região.
limitam uma região? Encontre a área da região.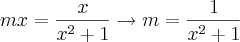

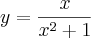 limitam uma região? Encontre a área da região.
limitam uma região? Encontre a área da região.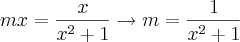

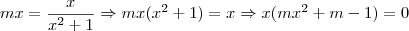
 e
e 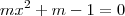 .
.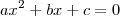 tem solução real quando
tem solução real quando 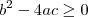 . Atenção! Cuidado ao identificar os coeficientes a, b e c da equação
. Atenção! Cuidado ao identificar os coeficientes a, b e c da equação 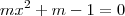 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

