olá abner,
uma forma da equação da reta é y = m*x + b (onde m é a inclinação). se vc isolar o y na equação que vc tem, a inclinação é o coeficiente que multiplica o x, ou seja:
3 x + 4 y = 5
 y =
y = 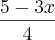
. se compararmos com y = m*x + b, percebemos que m = -3/4.
para traçar o gráfico de uma reta precisamos de dois pontos.
escolhendo x = 1 e substituindo na
equação acima, temos que y =
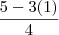
, logo y = 1/2. portanto o ponto (-1, 1) que vc disse
não está certo. o correto é o ponto (x,y) = (1, 1/2).
escolhendo x =0 (para facilitar nas contas), substituindo novamente, temos que y = 5/4. assim temos o segundo ponto (0, 5/4).
para traçar o gráfico vc encontra esses dois pontos no plano cartesiano com eixos (x, y), x na horizontal e y na vertical, e depois une os dois pontos. o gráfico não para na união dos dois pontos, então basta vc prolongar sobre a reta uma reta do tamanho que queira, que este será o gráfico da equação que você queria.
abraço



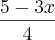
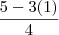 , logo y = 1/2. portanto o ponto (-1, 1) que vc disse
, logo y = 1/2. portanto o ponto (-1, 1) que vc disse  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.