Não consigo resolver esse exercicio da UF-MG, ele esta na parte de semelhança de triangulos do meu livro, e eu não achei nenhum outro exercicio parecido com ele ou que falasse de semicircuferência em triângulo, gostaria de uma ''luz'', para onde eu tenho que seguir e aonde eu encontraria algo relacionado a isso. Obrigado
P.S: a resposta do livro é r=a (raiz quadrada de dois - 1), o que me deixou mais confuso ainda :S
UF-MG Na figura ao lado, ABCD é um quadrado de lado a e F é o ponto de tangência da diagonal BD com a semicircufêrencia de centro E. Calcule o raio da semicircuferência em função de a.





![a\,\sqrt[]{2} a\,\sqrt[]{2}](/latexrender/pictures/9ef7b16167a4b0a6ee35c13e763e3e45.png) ,
,

![\frac{a\,\sqrt[]{2}}{a}=\frac{a-r}{r} \frac{a\,\sqrt[]{2}}{a}=\frac{a-r}{r}](/latexrender/pictures/31756da75fcb55a5c32aa1163d3351b5.png)
![\sqrt[]{2}=\frac{a-r}{r} \sqrt[]{2}=\frac{a-r}{r}](/latexrender/pictures/91d88a2b1d5324a5658cd1ac072948d3.png)
![r\,\sqrt[]{2}=a-r r\,\sqrt[]{2}=a-r](/latexrender/pictures/5466c38b055a8fea7557c342beed56eb.png)
![r(\sqrt[]{2}+1)=a r(\sqrt[]{2}+1)=a](/latexrender/pictures/1645a976c532103a8a033da35647adf9.png)
![r=\frac{a}{(\sqrt[]{2}+1)}*\frac{(\sqrt[]{2}-1)}{(\sqrt[]{2}-1)} r=\frac{a}{(\sqrt[]{2}+1)}*\frac{(\sqrt[]{2}-1)}{(\sqrt[]{2}-1)}](/latexrender/pictures/97a267f4f07f7767f5294b8b2b832aaf.png)
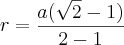
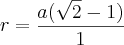
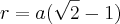


 .
.
 :
: