 por Civil UFSCar » Ter Jun 21, 2011 13:24
por Civil UFSCar » Ter Jun 21, 2011 13:24
PESSOAL, PRECISO DE AJUDA, NÃO CONSIGO DEDUZIR A ÁREA DO CÍRCULO!
EU COMECEI A FAZER:
![\int_{0}^{r}\sqrt[]{r^2-x^2} \int_{0}^{r}\sqrt[]{r^2-x^2}](/latexrender/pictures/d1fa31445f8c21af9241aaf5104c17bb.png)
dai, fiz o triângulo todo certinho e ficou assim:
hipotenusa=R
cateto oposto=x
cateto adjacente=
![\sqrt[2]{r^2-x^2} \sqrt[2]{r^2-x^2}](/latexrender/pictures/5772fc40fcd962f247efdb7526bf542d.png)
então, achei que dentro da raiz ficaria (1-sen²)
(lembrando que eu multiplicaria por 4r no fim pois eu calcularia somente 1/4 do círculo, e o r eu tirei de dentro da integral)
mas e agora o que eu faço?? depois de mudar o x^2/r^2 por sen, eu não sei o que eu coloco no intervalo de integração.
Agradeço a atenção de todos! Obrigado
-
Civil UFSCar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 20, 2011 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Molina » Ter Jun 21, 2011 15:02
por Molina » Ter Jun 21, 2011 15:02
O exercício quer que você deduza a fórmula da área do círculo através de integral?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Ter Jun 21, 2011 16:08
por LuizAquino » Ter Jun 21, 2011 16:08
Para resolver
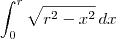
, você deve usar a técnica de substituição trigonométrica.
No caso, faça a substituição
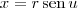
. Dessa forma,
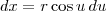
.
Alterando o intervalo de integração, para u = 0 temos x = 0 e para u = pi/2 temos x = r.
Desse modo, fazendo todas as simplificações, você precisa resolver:
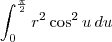
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área, círculo trigonométrico, equação (UFU)
 por Ananda » Qui Mar 06, 2008 11:51
por Ananda » Qui Mar 06, 2008 11:51
- 6 Respostas
- 9121 Exibições
- Última mensagem por Ananda

Qui Mar 06, 2008 17:48
Trigonometria
-
- Taxa de variacao - area do circulo !
por andersoneng » Sex Jun 29, 2012 10:40
- 2 Respostas
- 2928 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 21:18
Cálculo: Limites, Derivadas e Integrais
-
- A área do círculo determinado pela...
por David_Estudante » Sáb Mai 25, 2013 17:47
- 0 Respostas
- 1107 Exibições
- Última mensagem por David_Estudante

Sáb Mai 25, 2013 17:47
Geometria Analítica
-
- Dedução
por Guilherme Carvalho » Qua Ago 10, 2011 22:40
- 1 Respostas
- 1671 Exibições
- Última mensagem por Molina

Qua Ago 10, 2011 23:49
Trigonometria
-
- Dedução
 por silvanuno11 » Ter Mar 27, 2012 13:26
por silvanuno11 » Ter Mar 27, 2012 13:26
- 0 Respostas
- 1005 Exibições
- Última mensagem por silvanuno11

Ter Mar 27, 2012 13:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{r}\sqrt[]{r^2-x^2} \int_{0}^{r}\sqrt[]{r^2-x^2}](/latexrender/pictures/d1fa31445f8c21af9241aaf5104c17bb.png)
![\sqrt[2]{r^2-x^2} \sqrt[2]{r^2-x^2}](/latexrender/pictures/5772fc40fcd962f247efdb7526bf542d.png)



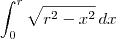 , você deve usar a técnica de substituição trigonométrica.
, você deve usar a técnica de substituição trigonométrica.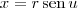 . Dessa forma,
. Dessa forma, 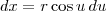 .
.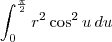 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
