na funçao f:R--->R tem-se uma parabola da funçao f(x+1)-f(x)=6x-2 entao o menor valor de f(x) é ?
obs:é eu pensava que ja vi de tudo de funçao de segundo grau.ficarei muito grato quem resolver!
por Fabricio dalla » Sex Jun 17, 2011 14:28
por LuizAquino » Dom Jun 19, 2011 12:40
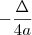. Esse valor ficará em função do coeficiente c.
por Fabricio dalla » Dom Jun 19, 2011 15:53
![f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2](/latexrender/pictures/abb3718cb039122094dcb3d793ac73ae.png "f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2")
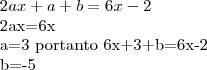
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)