 por -civil- » Qua Jun 15, 2011 23:04
por -civil- » Qua Jun 15, 2011 23:04
O plano  contém
contém
r : x - y = 0
x + z - 1 = 0
e determina, com os planos coordenados, um tetraedro de volume 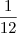 . Supondo que estamos num sistema ortogonal, obtenha os vértices do tetraedro e uma equação geral de
. Supondo que estamos num sistema ortogonal, obtenha os vértices do tetraedro e uma equação geral de  .
.O volume do tetraedro é

=
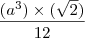
, sendo "a" a aresta do tetraedro
O volume dado é
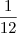
. Daí, igualando as equações

Eu transformei a equação de r para a forma vetorial e considerando x=

, obtive:
r: X = (0,0,1) +

(1,1,-1)
Eu considerei o mesmo ponto e vetor diretor da reta r, como o ponto e um dos vetores diretores de

mas eu preciso também de mais um vetor de

. Não sei como prosseguir.
Agradeço pela ajuda
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Jun 16, 2011 17:57
por LuizAquino » Qui Jun 16, 2011 17:57
O tetraedro do exercício não é regular (isto é, não é formado por triângulos equiláteros). Portanto, você não pode usar a fórmula para o volume como se todas as arestas fossem iguais.
Aqui vão três dicas:
(i) se
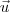
,

e
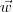
representam as arestas partindo de um mesmo vértice do tetraedro, então o seu volume é dado por
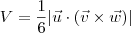
.
(ii) um dos vértices do tetraedro é a origem do sistema de coordenadas.
(iii) um dos vértices do tetraedro coincide com a interseção de r com o eixo z.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Vértices do tetraedro
por -civil- » Qua Ago 17, 2011 22:38
- 1 Respostas
- 2589 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 23:17
Geometria Analítica
-
- [PLANO] Equação Geral
por manuel_pato1 » Sex Set 21, 2012 19:54
- 3 Respostas
- 2987 Exibições
- Última mensagem por manuel_pato1

Sáb Set 22, 2012 11:50
Geometria Analítica
-
- Equação geral do plano
por lucash96 » Seg Nov 02, 2015 16:51
- 0 Respostas
- 1304 Exibições
- Última mensagem por lucash96

Seg Nov 02, 2015 16:51
Geometria Analítica
-
- Encontrar a Equação Geral do Plano
por Vitor2+ » Seg Nov 14, 2011 02:21
- 7 Respostas
- 10654 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:04
Geometria Analítica
-
- Tetraedro - Motivo que os vértices formam base e coordenadas
 por rochadapesada » Sáb Dez 14, 2013 21:29
por rochadapesada » Sáb Dez 14, 2013 21:29
- 7 Respostas
- 3219 Exibições
- Última mensagem por Russman

Dom Dez 15, 2013 14:18
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 contém
contém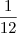 . Supondo que estamos num sistema ortogonal, obtenha os vértices do tetraedro e uma equação geral de
. Supondo que estamos num sistema ortogonal, obtenha os vértices do tetraedro e uma equação geral de  .
. =
= 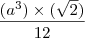 , sendo "a" a aresta do tetraedro
, sendo "a" a aresta do tetraedro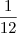 . Daí, igualando as equações
. Daí, igualando as equações 
 , obtive:
, obtive: (1,1,-1)
(1,1,-1) mas eu preciso também de mais um vetor de
mas eu preciso também de mais um vetor de  . Não sei como prosseguir.
. Não sei como prosseguir. 

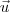 ,
,  e
e 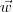 representam as arestas partindo de um mesmo vértice do tetraedro, então o seu volume é dado por
representam as arestas partindo de um mesmo vértice do tetraedro, então o seu volume é dado por 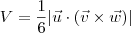 .
.

 .
.



