r : x + 2y + 2z - 3 = 0
x + z - 3 = 0 ,
P = (2, 1, 4) e s :
 , seja Q a projeção ortogonal de P sobre r. Supondo que o sistema adotado é ortogonal, obtenha o ponto A de s tal que a área de triângulo PQA seja 9.
, seja Q a projeção ortogonal de P sobre r. Supondo que o sistema adotado é ortogonal, obtenha o ponto A de s tal que a área de triângulo PQA seja 9.Eu passei a reta r para a forma vetorial e ficou desse jeito
r: X=

Fiz a mesma coisa com a reta s
s: X=

Para encontrar o ponto Q, eu pensei em usar a fórmula de projeção (Boulos, pg 67). Só que eu só posso utilizar vetores nessa fórmula. Daí eu usei o ponto da reta r, B=

Eu tenho que
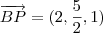 e
e 
Então

fazendo as contas, achei que
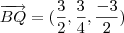
Como

encontrei

A partir daí como eu faço para encontrar o ponto A?
Agradeço pela ajuda


 está errado (e portanto
está errado (e portanto  .
.
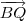 errado. Refazendo as contas, achei que
errado. Refazendo as contas, achei que 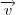 . Daí, Q=(1, -1,2). Depois calculando
. Daí, Q=(1, -1,2). Depois calculando  , cheguei que A pode ser (5,1,-2) ou
, cheguei que A pode ser (5,1,-2) ou 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)