Sub-seção para materiais das disciplinas relacionadas à Geometria.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por gustavoluiss » Seg Jun 13, 2011 18:57
por gustavoluiss » Seg Jun 13, 2011 18:57
Um avião voa a uma altitude de 500 m com

vetor de módulo de 200 m/s, numa região em que g = 10 m/s².
O piloto pretende soltar uma bomba que atinga um alvo situado no ponto P.Determine:
a)a distância D entre o ponto P e a reta vertical (r) que o passa pelo avião no momento em que a bomba é solta;b) o ângulo teta segundo o qual o piloto enxerga o alvo no momento em que a bomba é solta.Olá a questão a eu calculei sem problemas , agora a questão b eu não consigo resolver alguém poderia me explicar, porfavor?

-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Neperiano » Ter Jun 21, 2011 16:30
por Neperiano » Ter Jun 21, 2011 16:30
Ola
Primeiro calcule o outro angulo, não o teta, o 90 - teta. vou chamar de alfa
Ele é dado por:
tg alfa = D/500
O d vc calculou na letra a
Depois q axar esse angulo, faça 90 - ele e ira achar o outro
Axo que da para fazer assim, senaum teremos que tentar de otra forma
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Ter Jun 21, 2011 21:00
por MarceloFantini » Ter Jun 21, 2011 21:00
Se o seu desenho estiver certo, note que a trajetória do avião é paralela ao plano onde ele quer jogar a bomba. Usando geometria, temos que o ângulo embaixo do triângulo retângulo é

também, logo ele é tal que
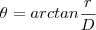
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Movimento Curvo] Questão fácil
por gustavoluiss » Ter Ago 23, 2011 14:19
- 10 Respostas
- 5711 Exibições
- Última mensagem por gustavoluiss

Qui Ago 25, 2011 00:11
Álgebra Elementar
-
- Movimento de uma partícula
por Cleyson007 » Sex Jul 27, 2012 16:17
- 1 Respostas
- 1548 Exibições
- Última mensagem por MarceloFantini

Sex Jul 27, 2012 16:56
Física
-
- Felino em movimento
por Cleyson007 » Qui Nov 01, 2012 18:58
- 2 Respostas
- 1882 Exibições
- Última mensagem por e8group

Qui Nov 01, 2012 20:02
Física
-
- Gráfico do movimento
por Cleyson007 » Qui Nov 01, 2012 19:14
- 1 Respostas
- 1583 Exibições
- Última mensagem por young_jedi

Qui Nov 01, 2012 20:04
Física
-
- Mala em movimento
 por Cleyson007 » Ter Jan 15, 2013 16:41
por Cleyson007 » Ter Jan 15, 2013 16:41
- 5 Respostas
- 6240 Exibições
- Última mensagem por Cleyson007

Qui Jan 17, 2013 09:02
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 vetor de módulo de 200 m/s, numa região em que g = 10 m/s².
vetor de módulo de 200 m/s, numa região em que g = 10 m/s².


 também, logo ele é tal que
também, logo ele é tal que 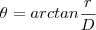 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

