 por Dalila » Qua Nov 19, 2008 14:09
por Dalila » Qua Nov 19, 2008 14:09
Numa P.A de dez termos o ultimo e igual a 22 e a razao e igual a dois.Determine o primeiro termo e a soma.
n=1,an=22,r=2
an=a1+(n-1)xr
22=a1+(10-1)x2
22=a1+a1+20-2
22=a1+18
a1=20-18
a1=4
-
Dalila
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Nov 14, 2008 14:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Qui Nov 20, 2008 16:13
por Neperiano » Qui Nov 20, 2008 16:13
Ola
Esta correta sim
Até
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sáb Nov 22, 2008 17:42
por Molina » Sáb Nov 22, 2008 17:42
Boa tarde, Dalila.
Só fazendo uma breve correção: o
n é igual a
10.
Dalila escreveu:n=1,an=22,r=2
Mas acredito que foi erro de digitação, já que você colocou corretamente na fórmula.

Já a segunda questão do problema (soma) você deve utilizar a Fórmula da Soma de uma PA:
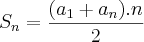
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Seg Nov 24, 2008 00:37
por admin » Seg Nov 24, 2008 00:37
Olá.
Apenas completando a correção (também acredito ter sido um descuido na edição):
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Essa elipse e essa parábola se encontram?
por Gregorio Diniz » Qua Mar 12, 2014 17:00
- 2 Respostas
- 1847 Exibições
- Última mensagem por Gregorio Diniz

Qua Mar 12, 2014 18:32
Geometria Analítica
-
- Resolução correta?
por Malorientado » Sáb Set 08, 2012 14:37
- 6 Respostas
- 4342 Exibições
- Última mensagem por vmo_apora

Dom Set 09, 2012 16:23
Matrizes e Determinantes
-
- Re: Derivada - Resposta correta?
por iceman » Dom Set 16, 2012 22:22
- 1 Respostas
- 1507 Exibições
- Última mensagem por MarceloFantini

Dom Set 16, 2012 22:27
Cálculo: Limites, Derivadas e Integrais
-
- Integrais feita, esta correta?
por Maykids » Qua Jun 22, 2011 13:50
- 4 Respostas
- 2842 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 24, 2011 00:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Está correta a resolução?
por Fabio Wanderley » Qui Nov 29, 2012 11:47
- 4 Respostas
- 3784 Exibições
- Última mensagem por Fabio Wanderley

Sex Nov 30, 2012 09:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





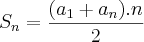



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
