Pessoal, acho que ja estou fazendo bagunça nas derivadas.Por gentileza me ajudem!!!
1)Prove usando as regras de seno e cosseno que a derivada de:
a)y= cotg x é y'=
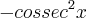
Minha tentativa (falida):
y=
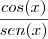
Aí tentei aplicar a regra do quociente:
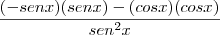
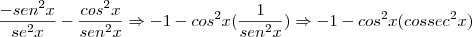
Ou seja, fiz uma bagunça! Alguem pode me ajudar por gentileza?
![\frac{-[(sen^2x) + (cos^2x)]}{sen^2x}\Rightarrow \frac{-1}{sen^2x}\Rightarrow-cossec^2 x](/latexrender/pictures/6c5d1e27a244e7d311225e02f71fb7a0.png "\frac{-[(sen^2x) + (cos^2x)]}{sen^2x}\Rightarrow \frac{-1}{sen^2x}\Rightarrow-cossec^2 x")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)