Uma lata cilíndrica de estanho (sem tampa) tem volume de 5 centímetros cúbicos. Determine suas dimensões se a quantidade de estanho para a fabricação da lata é mínima.
Nao sei por onde começar!!!



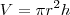 . Nesse exercício, temos que
. Nesse exercício, temos que  cm³.
cm³.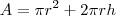 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

