Obrigado
Questão: Encontre o valor de ' y ':
![g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ] g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ]](/latexrender/pictures/0cbac1579cac5e04cc34d983d1c2880b.png)

![g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ] g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ]](/latexrender/pictures/0cbac1579cac5e04cc34d983d1c2880b.png)

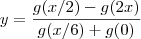
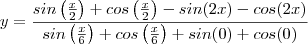
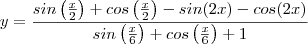



wallsoares escreveu:Diego, Muito obrigado pela atenção, porém foi exatamente nesse ponto em que eu empaquei quando criei o tópico =).
Será que não poderia dar mais um passinho apenas? Depois eu me viro.
Obrigado.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)