 por aline_n » Qua Jun 01, 2011 20:14
por aline_n » Qua Jun 01, 2011 20:14
como acho o numero critico dessa funcao??
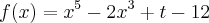
Estou com dificuldade devido a letra t aparecer.....
-
aline_n
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 28, 2011 09:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por carlosalesouza » Qua Jun 01, 2011 22:30
por carlosalesouza » Qua Jun 01, 2011 22:30
não deixe ela te assustar.... rs
A não ser que t represente um termo de x, basta fazer a derivação... como t é um monômio de grau 1, sua derivada será 1...
Então, a derivada ficará:
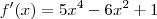
De repente eu to falando bobagem... hehehehe
Mas creio que os números críticos serão as raizes desse polinômio...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por guermandi » Qui Jun 02, 2011 10:57
por guermandi » Qui Jun 02, 2011 10:57
Eu acho que a função eh função apenas de x
quando vc deriva em relação a x , nao pode derivar o t tb
t deve ser um parametro e assim a resposta fica em função de t
-
guermandi
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Jun 01, 2011 10:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por carlosalesouza » Qui Jun 02, 2011 11:45
por carlosalesouza » Qui Jun 02, 2011 11:45
Com certeza... sendo t uma variável em função de x, ou seja, t(x), precisaríamos encontrar a derivada de t...
Novamente, posso estar falando bobagem... derivando passo a passo:
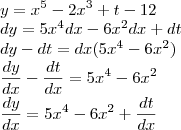
Ou seja, a derivada de y em função de x é

somado à derivada de t em função de x...
Luiz!!!! Dá uma LUZ!!! heheheh
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 15:39
por LuizAquino » Qui Jun 02, 2011 15:39
É necessário saber qual é o texto do exercício na íntegra.
Do jeito que está, sem qualquer informação adicional, como a variável independente da função é
x (já que a função está escrita como
f(
x)), então
t deve ser considerado como uma constante (isto é, um número qualquer que
não depende de x).
Desse modo, a função
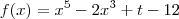
tem derivada dada por
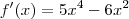
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carlosalesouza » Qui Jun 02, 2011 18:33
por carlosalesouza » Qui Jun 02, 2011 18:33
De fato, sendo t um valor independente, ele vai deslocar o valor de y, não de x... então, o x crítico será sempre o mesmo... ou seja, as 4 raizes reais da derivada...
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros criticos!!!
 por aline_n » Qua Jun 01, 2011 18:59
por aline_n » Qua Jun 01, 2011 18:59
- 1 Respostas
- 1368 Exibições
- Última mensagem por carlosalesouza

Qua Jun 01, 2011 19:19
Cálculo: Limites, Derivadas e Integrais
-
- Números Críticos
 por Cleyson007 » Ter Jan 28, 2014 18:42
por Cleyson007 » Ter Jan 28, 2014 18:42
- 5 Respostas
- 2741 Exibições
- Última mensagem por Cleyson007

Qua Jan 29, 2014 08:11
Cálculo: Limites, Derivadas e Integrais
-
- Números Críticos
por Carolwis » Sáb Nov 15, 2014 14:39
- 1 Respostas
- 1505 Exibições
- Última mensagem por adauto martins

Qua Nov 19, 2014 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Números críticos da função
por Vencill » Ter Dez 02, 2014 17:38
- 1 Respostas
- 1226 Exibições
- Última mensagem por Cleyson007

Ter Dez 02, 2014 18:04
Funções
-
- Determinar os numeros criticos
por Vencill » Qua Dez 03, 2014 17:42
- 3 Respostas
- 1905 Exibições
- Última mensagem por Cleyson007

Qui Dez 04, 2014 08:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
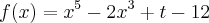

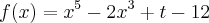

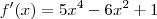


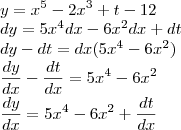
 somado à derivada de t em função de x...
somado à derivada de t em função de x...
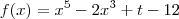 tem derivada dada por
tem derivada dada por 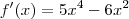 .
.
