 por maria cleide » Sáb Mai 28, 2011 16:36
por maria cleide » Sáb Mai 28, 2011 16:36
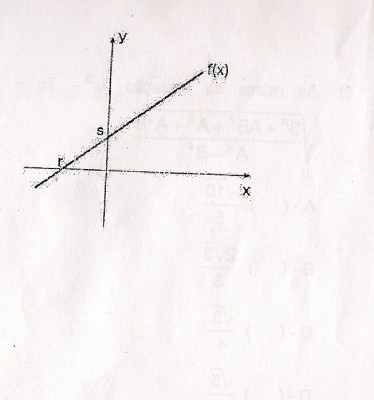
Analise as afirmativas referentes à função afim representada no gráfico anexo:
I. A função é crescente.
II. Se x>r então f(x)<0.
III. s representa o termo independente da função.
IV. A declividade da reta é dada por r.
A alternativa que corresponde às afirmativas corretas é:
A-( ) I e III
B-( ) I e II
C-( ) I e IV
D-( ) II e III
Sei que I é correta pois a função é crescente; II é incorreta pois se x>r então f(x)>0 e não < que 0; Já as outras duas não sei, consequentemente não consigo encontrar a resposta.
- Anexos
-
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Sáb Mai 28, 2011 17:49
por MarceloFantini » Sáb Mai 28, 2011 17:49
Primeira é correta, segunda é incorreta. Perceba que se supormos
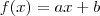
, sabemos que

, logo, s é o termo independente da função, logo correta. Note por último que se fizer o coeficiente angular não terá apenas r, portanto falsa. Resposta A.
Editado pela última vez por
MarceloFantini em Dom Mai 29, 2011 19:40, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Dom Mai 29, 2011 18:37
por maria cleide » Dom Mai 29, 2011 18:37
s ou r é o termo independente da função?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Dom Mai 29, 2011 19:41
por MarceloFantini » Dom Mai 29, 2011 19:41
Peço desculpas, já arrumei.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida sobre função.
por ibatexano » Ter Out 06, 2009 19:00
- 5 Respostas
- 3296 Exibições
- Última mensagem por jwcosta

Dom Out 25, 2009 20:11
Funções
-
- Função sobre lado
por pedro22132938 » Dom Mar 22, 2015 17:17
- 1 Respostas
- 2967 Exibições
- Última mensagem por Russman

Seg Mar 23, 2015 02:00
Funções
-
- dúvida sobre função derivável
por MariPC » Sáb Ago 15, 2009 14:45
- 6 Respostas
- 6340 Exibições
- Última mensagem por MarceloFantini

Sex Jun 03, 2011 16:02
Cálculo: Limites, Derivadas e Integrais
-
- duvida sobre função continua
por levyrc » Sex Abr 08, 2011 22:56
- 2 Respostas
- 2319 Exibições
- Última mensagem por LuizAquino

Dom Abr 10, 2011 13:24
Funções
-
- Dúvidas sobre Função Quadrática
por Aroldo » Ter Jun 21, 2011 20:35
- 4 Respostas
- 3015 Exibições
- Última mensagem por Aroldo

Ter Jun 21, 2011 22:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


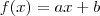 , sabemos que
, sabemos que  , logo, s é o termo independente da função, logo correta. Note por último que se fizer o coeficiente angular não terá apenas r, portanto falsa. Resposta A.
, logo, s é o termo independente da função, logo correta. Note por último que se fizer o coeficiente angular não terá apenas r, portanto falsa. Resposta A.

