Dúvida - resolução função !

[jamiel]

Determine a equação da função representada pela parte de baixo da curva . Qual o domínio dessa função?

Nos meus calculos deu uma parábola com o bico voltado para a direita:



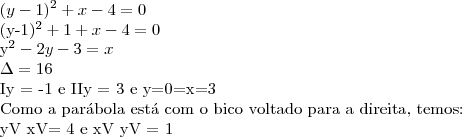
Nesse caso a equação da parte de baixo da curva fica:
3a - 1 = y

(1/3)x - 1 = y

O domínio é D = {x ? R| x = 3}


Alguém para dar uma dica quanto a essa resolução?

[FilipeCaceres]

Vou postar a forma que eu resolveria.
que representa uma parábola rotacionada.

Desenvolvendo temos,



Logo, devemos ter:


Portanto,

[jamiel]

Quer dizer q esse x ? 4 é o domínio?

Pq o 4 é o limite da parábola, o bico apontando para o lado direito. Quer dizer q eu errei o domínio?
vlw ....

[FilipeCaceres]

Quer dizer q esse x ? 4 é o domínio?

Sim.

Pq o 4 é o limite da parábola, o bico apontando para o lado direito

.

Observe a função , para que ela exista devemos devemos ter

[jamiel]

Mas, o meu método está certo ou tem alguma falha(falo em relação a resolução)?

[FilipeCaceres]

Eu calculei o domínio desta função

Mas agora eu reli o enunciado e vi que ele pede o domínio de um função que está abaixo da curva.

Determine a equação da função representada pela parte de baixo da curva . Qual o domínio dessa função?

Posso estar errado, mas acredito que está faltanto ele dar um ponto.

[jamiel]

Pois, é. A parte de baixo do gráfico dessa função não seria y=-1 e x = 3. a seria 1/3, ficaria, então: (1/3)x -1 = 0, com x = 3, o domínio?

[FilipeCaceres]

Pode ser que quando ele diz:

função representada pela parte de baixo da curva

esteja se referindo a "perna" inferior da parábola e desta forma a minha solução apresentada também é válida.

Ou seja,
O domínio é D ={}

[FilipeCaceres]

parabola.gif (2.64 KiB) Exibido 5934 vezes

Observe a figura,o ponto x=3 na verdade é o ponto onde o gráfico cruza o eixo x.

[jamiel]

Isso é o q poderiamos chamar de "domínio total" da função? Pq se olharmos bem, o 3 corta o eixo "x". Então, neste caso, em particular, seria 4 mesmo, q é o valor máximo até onde a reta vai, não é?

[FilipeCaceres]

Ele não te deu internalo, logo o o que se quer é o domínio da função formada por toda parte inferior da curva.

[jamiel]

Caramba! É verdade, o 3 é o valor q corta o eixo apenas. Mas fiquei pensando se ele só quer a parte de baixo, por mais q o bico da parábola vá até o x=4, sem cortar o eixo, a reta se constitui de y=-1 e x=3. Mas pensando bem, essa mesma reta só vai até 4. Logo, D={x ? R| x ? 4}. Esse seria o raciocínio?