 por demolot » Qua Mai 25, 2011 13:04
por demolot » Qua Mai 25, 2011 13:04
Boa tarde a toda a comunidade tenho um pequeno problema, o exercicio é o seguinte:

Sabendo que F é diferenciável, mostre que
?u/?y cos(x) + ?u/?x cos(y) = cos(x)*cos(y)
eu nao tenho a mais pequena ideia como isto se faz, no caderno do prof nao esta nenhuma deste tipo, eu nem sei se é bem pela regra da derivaçao da composta, alguem me pode dar umas orientaçoes, gostava so de orientaçoes nao da resposta muito obrigado desde ja
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por LuizAquino » Qua Mai 25, 2011 23:42
por LuizAquino » Qua Mai 25, 2011 23:42
Qual é exatamente o texto original do exercício?
A função
u não seria
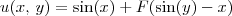
?
De qualquer modo, para resolver um exercício desse tipo você precisa saber calcular derivadas parciais além de saber a Regra da Cadeia para funções com várias variáveis. Você já estudou esses conteúdos?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por demolot » Qui Mai 26, 2011 07:04
por demolot » Qui Mai 26, 2011 07:04
sim ja dei essa materia, o enunciado é so este:
4. Considere a seguinte função
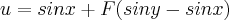
.
Sabendo que F é diferenciável, mostre que
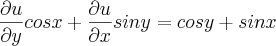
sera que tem alguma coisa a ver com a diferencibilidade da funçao F?
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por LuizAquino » Qui Mai 26, 2011 12:29
por LuizAquino » Qui Mai 26, 2011 12:29
Note que o exercício está diferente nas duas mensagens que você enviou!
De qualquer modo, eu sugiro que você arrume o exercício da seguinte maneira. Considere que
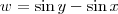
. Se a segunda expressão para a função
u é a correta, então você ficará com:
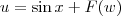
.
Agora, lembre-se que:
![\frac{\partial u}{\partial y} = \frac{\partial [\sin x + F(w)]}{\partial y} = \frac{\partial (\sin x)}{\partial y} + \frac{d F}{dw}\frac{\partial w}{\partial y} \frac{\partial u}{\partial y} = \frac{\partial [\sin x + F(w)]}{\partial y} = \frac{\partial (\sin x)}{\partial y} + \frac{d F}{dw}\frac{\partial w}{\partial y}](/latexrender/pictures/66270f50c845a91cd2a23ea31077ccef.png)
,
![\frac{\partial u}{\partial x} = \frac{\partial [\sin x + F(w)]}{\partial x} = \frac{\partial (\sin x)}{\partial x} + \frac{d F}{dw}\frac{\partial w}{\partial x} \frac{\partial u}{\partial x} = \frac{\partial [\sin x + F(w)]}{\partial x} = \frac{\partial (\sin x)}{\partial x} + \frac{d F}{dw}\frac{\partial w}{\partial x}](/latexrender/pictures/c6c8715670ab27bb43a26e02780a575b.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por demolot » Qui Mai 26, 2011 12:55
por demolot » Qui Mai 26, 2011 12:55
muito obrigado pela resposta, esta correcto

fiz as contas e deu a demonstração pedida
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada e composta]
por Saruka » Sex Nov 11, 2011 18:26
- 2 Respostas
- 1427 Exibições
- Última mensagem por LuizAquino

Qui Nov 17, 2011 17:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - função composta
por core » Qua Out 16, 2013 15:54
- 1 Respostas
- 1335 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de função composta
por Fernandobertolaccini » Qua Jul 09, 2014 08:37
- 0 Respostas
- 914 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 09, 2014 08:37
Cálculo: Limites, Derivadas e Integrais
-
- derivada de função composta.
por nandooliver008 » Dom Set 21, 2014 19:42
- 1 Respostas
- 1229 Exibições
- Última mensagem por Cleyson007

Seg Set 22, 2014 18:04
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1956 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



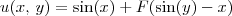 ?
?
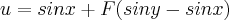 .
.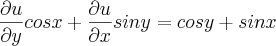
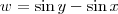 . Se a segunda expressão para a função
. Se a segunda expressão para a função 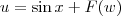 .
.![\frac{\partial u}{\partial y} = \frac{\partial [\sin x + F(w)]}{\partial y} = \frac{\partial (\sin x)}{\partial y} + \frac{d F}{dw}\frac{\partial w}{\partial y} \frac{\partial u}{\partial y} = \frac{\partial [\sin x + F(w)]}{\partial y} = \frac{\partial (\sin x)}{\partial y} + \frac{d F}{dw}\frac{\partial w}{\partial y}](/latexrender/pictures/66270f50c845a91cd2a23ea31077ccef.png) ,
,![\frac{\partial u}{\partial x} = \frac{\partial [\sin x + F(w)]}{\partial x} = \frac{\partial (\sin x)}{\partial x} + \frac{d F}{dw}\frac{\partial w}{\partial x} \frac{\partial u}{\partial x} = \frac{\partial [\sin x + F(w)]}{\partial x} = \frac{\partial (\sin x)}{\partial x} + \frac{d F}{dw}\frac{\partial w}{\partial x}](/latexrender/pictures/c6c8715670ab27bb43a26e02780a575b.png) .
.