por jamiel » Seg Mai 23, 2011 21:54
Expresse a área superficial de um cubo como função do seu volume.
A = 6*x² e V = x*x² ou x^3
Se fosse o cont rário, seria assim:
V(A) = x*x² = (x²=A/6) ---> (A/6)*(?A/6) ---> f(x) = (x/6)*(?x/6), mas se eu fizer o q o enunc iado pede, ao mesmo modo da resolução anterior, não consigo:
Ex:
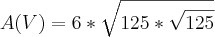
Não estou conseguindo o resultado satisfatório, alguém tem alguma dica para resolver isso?
-
jamiel
- Colaborador Voluntário
-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
por jamiel » Seg Mai 23, 2011 22:54
Eu acho q não-posso estar enganado-
O q o enunciado pede é : área como função do volume ! Mas, vlw!
-
jamiel
- Colaborador Voluntário
-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
por MarceloFantini » Seg Mai 23, 2011 23:06
Área como função do volume significa mostrar uma relação onde a área depende apenas do volume, certo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por FilipeCaceres » Seg Mai 23, 2011 23:17
Olá Marcelo,
Não entendi a sua função.
Observe que:
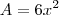
![V=x^3\,\therefore x=\sqrt[3]{V}](/latexrender/pictures/bfe600616dc7c28b1115b82e09c67dca.png "V=x^3\,\therefore x=\sqrt[3]{V}")
Logo temos,
![A=6.\sqrt[3]{V^2}](/latexrender/pictures/894219b5934a1182dad1fedca96d3347.png "A=6.\sqrt[3]{V^2}")
Não seria isto?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por MarceloFantini » Seg Mai 23, 2011 23:25
Minha álgebra ficou incompleta, deve resultar no mesmo. Estou cansado e preguiçoso no momento, hauhahu.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por jamiel » Seg Mai 23, 2011 23:57
Felipe, na mosca! rsrsr
Muito obrigado aos dois, de qualquer maneira! Agora, irei dar uma olhada nessa resolução. abçsss!
-
jamiel
- Colaborador Voluntário
-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
por jamiel » Ter Mai 24, 2011 00:01
Felipe, como vc chegou nesta função? rsrsrs
Essa foi tensa!
-
jamiel
- Colaborador Voluntário
-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
por FilipeCaceres » Ter Mai 24, 2011 00:07
Olá jamiel,
Observe o que eu fiz.
Sabemos que:
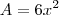
(i)
(ii)
Eu isolei o valor de x em (ii) e substitui em (i), assim temos,
![A=6.(\sqrt[3]{V})^2](/latexrender/pictures/fd06720af0249770400109d33edabe20.png "A=6.(\sqrt[3]{V})^2")
Então,
Abraço
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por jamiel » Ter Mai 24, 2011 00:48
Valeu, mesmo! Dei uma analisada aqui e ach o q entendi !
![f(x) = 6*{(\sqrt[3]{x})}^{2}](/latexrender/pictures/f95549f45d5fe74dc221d624014d509f.png "f(x) = 6*{(\sqrt[3]{x})}^{2}")
Deu certinho aqui!
Thank you a lot!
-
jamiel
- Colaborador Voluntário
-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função - Resolução(ajuda)
por jamiel » Seg Mai 23, 2011 01:13
- 6 Respostas
- 3306 Exibições
- Última mensagem por jamiel
Seg Mai 23, 2011 13:48
Funções
-
- Exercício de função para ajuda na resolução.
por MARCION » Seg Dez 15, 2014 13:31
- 3 Respostas
- 2181 Exibições
- Última mensagem por Russman
Seg Dez 15, 2014 19:56
Funções
-
- Ajuda com a resolução
por Mimizinha » Qua Mar 19, 2008 14:40
- 2 Respostas
- 3358 Exibições
- Última mensagem por Mimizinha
Qui Mar 20, 2008 13:18
Álgebra Elementar
-
- ajuda com resolução do problema
por Mimizinha » Qua Mar 19, 2008 16:46
- 2 Respostas
- 2458 Exibições
- Última mensagem por Mimizinha
Qua Mar 19, 2008 17:34
Geometria Plana
-
- Ajuda com resolução do exercicio
por Mimizinha » Ter Abr 01, 2008 10:27
- 3 Respostas
- 5618 Exibições
- Última mensagem por admin
Ter Abr 01, 2008 23:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
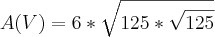
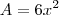![V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}](/latexrender/pictures/732927c7d66cda95fc2558031bce67eb.png "V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}")
![A=6x^2, V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}](/latexrender/pictures/65049ee8aa3ae07d85dfae90d8f66d09.png "A=6x^2, V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}")